Dénombrement à l'aide d'arbres et de tableaux
Dénombrement à l’aide d’arbres et de tableaux
Le dénombrement consiste à compter le nombre d’éléments d’un ensemble donné. Les principales sources d’erreurs lors d’un tel procédé sont de compter plusieurs fois le même élément ou d’en oublier.
1 – Diagramme de Venn
Dans une classe, deux langues vivantes sont proposées.
20 élèves font de l’anglais, 18 font de l’espagnol et 4 élèves étudient les deux.
Tous les élèves étudient au moins une langue. Quel est le nombre total d’élèves ?
L’erreur serait ici d’ajouter le nombre d’élèves pratiquant l’anglais et le nombre d’élèves pratiquant l’espagnol, en recomptant ici deux fois les élèves qui étudient les deux langues.
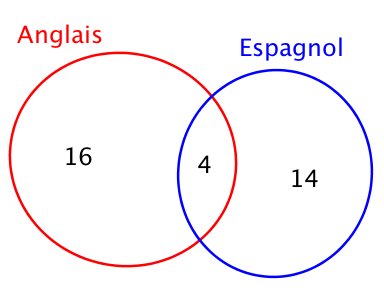
On représente en rouge les élèves pratiquant l’anglais et en bleu des élèves pratiquant l’espagnol : un groupe d’élèves appartient à ces deux ensembles.
On sait qu’il y a 20 élèves qui étudient l’anglais dont 4 qui étudient les deux langues.
Il a donc $20 – 4 = 16$ élèves qui étudient uniquement l’anglais.
On sait déplus qu’il y a 18 élèves qui étudient l’espagnol dont 4 qui étudient les deux langues.
Il a donc $18 – 4 = 14$ élèves qui étudient uniquement l’espagnol.
A l’intersection des deux ensembles, on indique alors le nombre d’élèves pratiquant les deux langues : 4.
On retrouve alors le nombre d’élèves pratiquant l’anglais ($16 + 4$) et l’espagnol ($14 + 4 = 18$).
Pour obtenir le nombre total d’élèves, on ajoute les nombres du diagramme : $16 + 4 + 14 = 34$.
2 – Tableau de Cantor
Sur 100 personnes, 68 sont des hommes, 43 d’entre eux sont végétariens. 12 de personnes sont des femmes non végétariennes.
Combien y-a-t-il de végétariens ?
On utilise alors un tableau de Cantor, c’est à dire un tableau à double entrées.
On indique sur les lignes le sexe des personnes et sur les colonnes le fait d’être végétarien ou non. On écrit en rouge les éléments présents dans l’énoncé.
On sait qu’il y a 68 hommes, on l’inscrit donc à l’intersection de la ligne Homme et de la colonne Total.
On sait aussi que 43 hommes sont végétariens.
L’effectif total est de 100.
Enfin, on sait que 12 femmes sont végétariennes.
On remplit alors le reste du tableau.
On obtient l’effectif des femmes en effectuant la différence de 100 et de 68, c’est à dire 32.
On peut alors obtenir le nombre de femmes végétariennes : $32 – 12 = 20$.
On sait alors le nombre de personnes végétariennes : $43 + 20 = 63$.
On en déduit alors le nombre de personnes non végétariennes : $100 = 63 = 27$.
Enfin, on trouve le nombre d’hommes non végétariens ; $68 – 43 = 25$.
| Végétariens ? | OUI | NON | TOTAL |
| Hommes | 43 | 25 | 68 |
| Femmes | 20 | 12 | 32 |
| Total | 63 | 37 | 100 |
Finalement, il y a donc 63 végétariens.
3 – Arbres
Un restaurant propose au choix deux entrées, trois plats principaux et deux desserts.
On cherche le nombre de menus possibles.
On modélise par deux branches le choix possible pour les entrées, $E_1$ et $E_2$.
A chacune des extrémités des entrées partent trois branches représentant les trois choix possibles $P_1$, $P_2$ et $P_3$ des plats principaux.
Enfin, à chacune des extrémités, on dessine deux branches pour les deux choix de desserts.
Chaque chemin de l’arbre est assimilable à un choix de menu.
Pour trouver le nombre $N$ de menus, il suffit de compter le nombre de chemins, et il est plus simple de compter uniquement les extrémités de ces chemins.
$N=2\times 3\times 4=12$
On trouve alors $12$ menus possibles.


