Vecteurs et alignement
Vecteurs et alignement
Méthodes :
Il existe plusieurs méthodes pour montrer que des points sont alignés. Par exemple, il est possible d’utiliser les coefficients directeurs de droites. Mais on peut aussi utiliser les vecteurs.
Pour rappel, deux points sont toujours alignés.
Méthode utilisant les vecteurs.
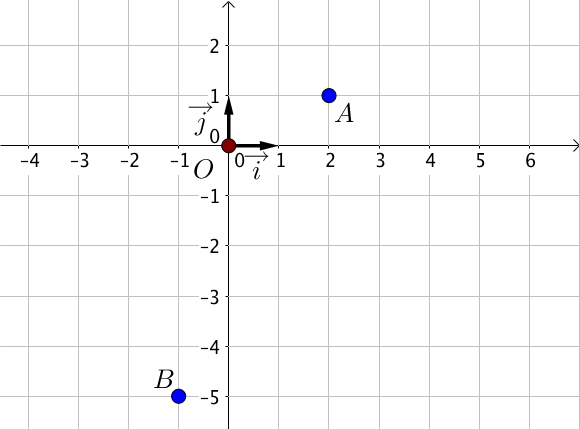
On se place dans un repère $(O; \overrightarrow{i}; \overrightarrow{j})$.
Soient $A(2; 1), B(-1: -5)$ et $C(10; 17)$ trois points du plan,
$A, B$ et $C$ sont-ils alignés ?
La méthode consiste à former deux vecteurs en utilisant les points dont on cherche à démontrer l’alignement en veillant à ce que ces deux vecteurs aient un point en commun.
Pour que les points soient alignés, il faudrait donc que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ par exemple soient colinéaires.
En effet, cela impliquerait que les droites $(AB)$ et $(AC)$ sont parallèles, avec un point en commun $A$ : les points $A, B$ et $C$ seraient ainsi alignés.
Calculons donc les coordonnées de ces deux vecteurs :
$\overrightarrow{AB} \left ( \begin{array}{c} -1 – 2 \\ -5 -1 \end{array} \right )$
c’est à dire $\overrightarrow{AB} \left ( \begin{array}{c} -3 \\ -6 \end{array} \right )$
$\overrightarrow{AC} \left ( \begin{array}{c} 10 – 2 \\ 17 -1 \end{array} \right )$
c’est à dire $\overrightarrow{AC} \left ( \begin{array}{c} 8 \\ 16 \end{array} \right )$
Pour étudier la colinéarité des deux vecteurs, on peut calculer séparément le rapport des abscisses puis le rapport des ordonnées des deux vecteurs.
Ainsi, $\dfrac{8}{-3} = -\dfrac{8}{3}$ et $\dfrac{16}{-6} = -\dfrac{8}{3}$.
Donc $\overrightarrow{AC} = -\dfrac{8}{3} \overrightarrow{AB}$ : ces deux vecteurs sont donc colinéaires.
On peut aussi remarquer dans ce cas là que l’on peut réécrire le vecteur $\overrightarrow{AB}$ comme $\overrightarrow{AB} = -3 \overrightarrow{u}$, avec $\overrightarrow{u} \left ( \begin{array}{c} 1 \\ 2 \end{array} \right )$.
De même, $\overrightarrow{AC} = 8 \overrightarrow{u}$.
Ainsi, $\overrightarrow{AB}$ et $\overrightarrow{u}$ sont colinéaires, de même que $\overrightarrow{AC}$ et $\overrightarrow{u}$ :
donc, $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.
Dans les deux cas, les droites $(AB)$ et $(AC)$ sont donc parallèles et possèdent un point commun $A$, les points sont donc alignés.
Somme de vecteurs, relation de Chasles
Somme de vecteurs, relation de Chasles
1) Préliminaires
Soient $A, B$ et $C$ trois points du plan,
$\overrightarrow{AA} = \overrightarrow{0}$, c’est à dire le vecteur nul. Il n’a pas de direction ni de sens et sa norme vaut 0.
Il faudra bien écrire une flèche sur ce vecteur pour le différencier du nombre 0.
$\overrightarrow{AB} = -\overrightarrow{BA}$, lorsque l’on change de sens d’un vecteur, ce nouveau vecteur est l’opposé du vecteur initial.
2) Représentation graphique
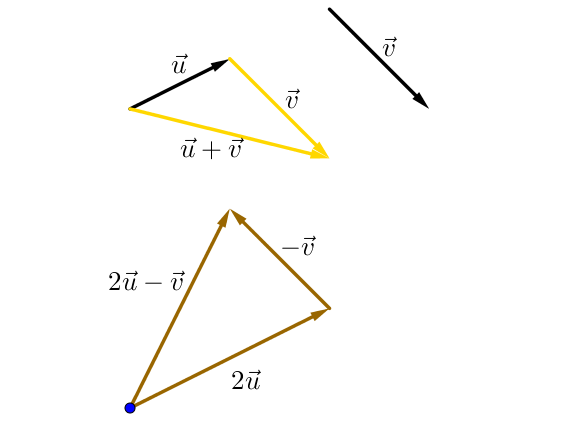
a) Représentons le vecteur $\overrightarrow{u} + \overrightarrow{v}$. (en noir sur la figure)
On remarque que ses vecteurs sont déjà tracés. Pour effectuer la somme, on souhaite que la flèche du vecteur $\overrightarrow{u}$ coïncide avec le début du vecteur $\overrightarrow{v}$.
Il faut donc déplacer le vecteur $\overrightarrow{v}$. Or on sait que deux vecteurs sont égaux si ils forment un parallélogramme.
On reporte donc le vecteur $\overrightarrow{v}$ en gardant le même sens, la même direction et la même norme : bien que ces deux vecteurs ne soient pas représentés au même endroit, ils sont égaux.
b) On souhaite à présent représenter le vecteur $2\overrightarrow{u} – \overrightarrow{v}$ ou encore $2\overrightarrow{u} + (-\overrightarrow{v})$.
On commence donc par tracer le vecteur $2\overrightarrow{u}$. Le vecteur $- \overrightarrow{v}$ est le vecteur de sens opposé à $ \overrightarrow{v}$.
On reporte donc le vecteur $- \overrightarrow{v}$ qui a la même norme que le vecteur $ \overrightarrow{v}$ représenté mais un sens opposé. On relie enfin le point de départ et le point d’arrivé.
3) Relation de Chasles
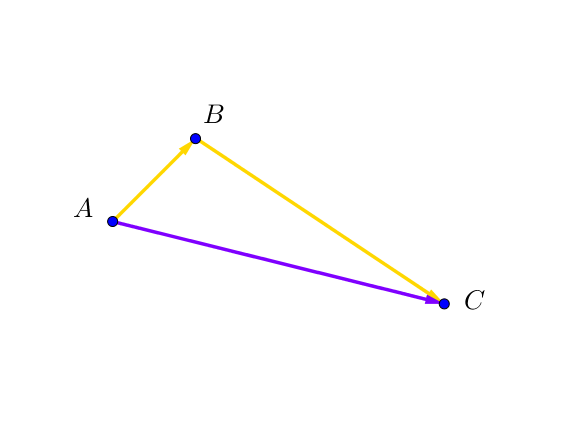
Enfin, on addition les vecteurs $\overrightarrow{AB} $ et $\overrightarrow{BC}$.
Graphiquement, on obtient le vecteur $\overrightarrow{AC}$ : c’est la relation de Chasles.
$\overrightarrow{AB} +\overrightarrow{BC}=\overrightarrow{AC}$