Point d'inflexion
Point d’inflexion
Définition
Un point d’inflexion d’une courbe est un point où la courbe traverse sa tangente.
Il s’agit d’une définition visuelle.
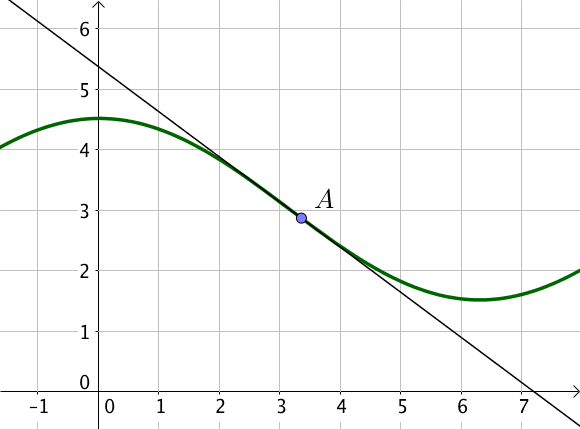
L’exemple qui suit représente un point d’inflexion au point $A$ car la courbe traverse sa tangente au point $A$ : elle est d’abord en dessous de sa tangente qui croise sa tangente au point $A$ et passe au dessus ensuite.
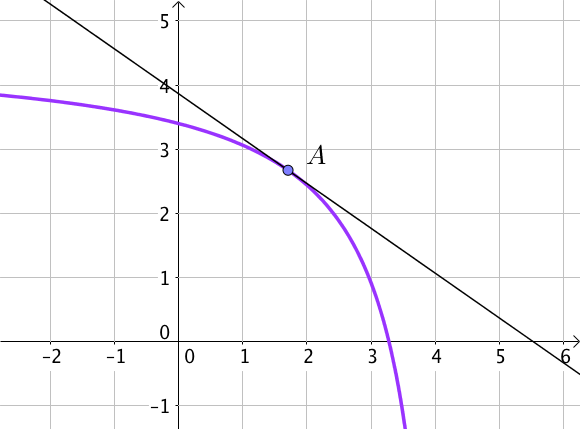
L’exemple ci-dessous montre que $A$ n’est pas un point d’inflexion : la courbe ne traverse pas sa tangente au point $A$ et reste toujours en dessous de cette dernière.
Exemple à connaitre :
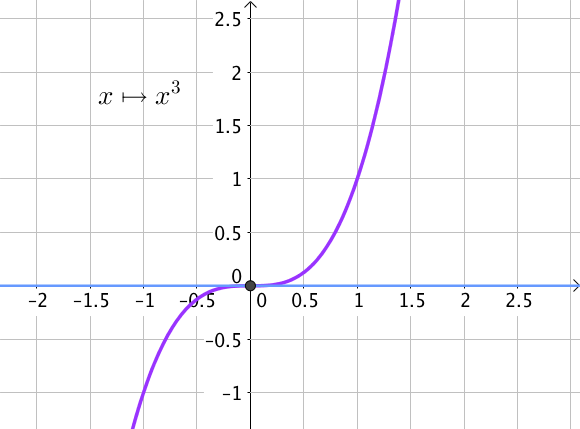
Parmi les fonctions usuelles, une fonction possède un point d’inflexion et constitue un exemple classique : c’est la fonction cube.
O l’origine du repère est un point d’inflexion.
En effet, pour $x \in \mathbb{R}, f'(x) = 3x^2$ donc $f'(0) = 0$.
De plus, la courbe traverse la tangente en ce point donc O est bien un point d’inflexion.
Positions relatives des courbes
Positions relatives des courbes
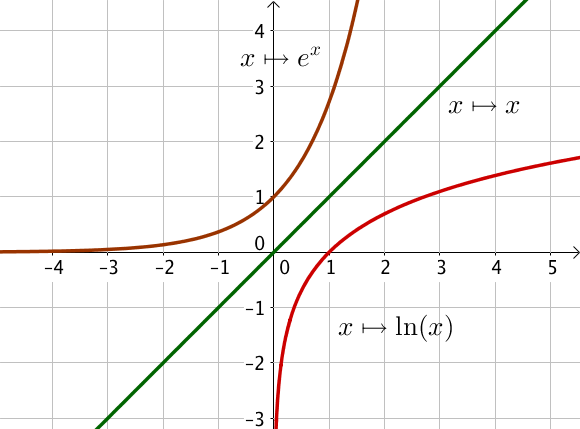
On trace les trois courbes représentatives des fonctions $x \mapsto x$, $x \mapsto \ln(x)$ et $x \mapsto e^x$.
Graphiquement, on remarque que la courbe représentative de la fonction exponentielle est au dessus de la courbe de la fonction $x \mapsto x$, elle même au dessus de la courbe représentative de la fonction logarithme népérien.
On peut alors en déduire l’inégalité suivante, à connaitre, et qui se retrouve facilement à l’aide d’un graphique :
Pour $x \in ]0; +\infty[$, on a :
$\ln(x) \leq x \leq e^x$.
On remarquera que cette inégalité n’est vraie que pour $x \in ]0; +\infty[$ car le logarithme népérien n’est pas défini pour des valeurs de $x$ négatives.
Outil pour trouver un point d'inflexion
Outil pour trouver un point d’inflexion
Théorème :
Soit $f$ une fonction définie sur $]a; b[$ telle que $f”$ existe sur $]a; b[$ et $x_0$ un point de l’intervalle $]a; b[$,
si $f”$ s’annule en $x_0$, en changeant de signe alors le point $M_0(x_0, f(x_0))$ est un point d’inflexion.
Exemple :
Soit $f$ la fonction définie par
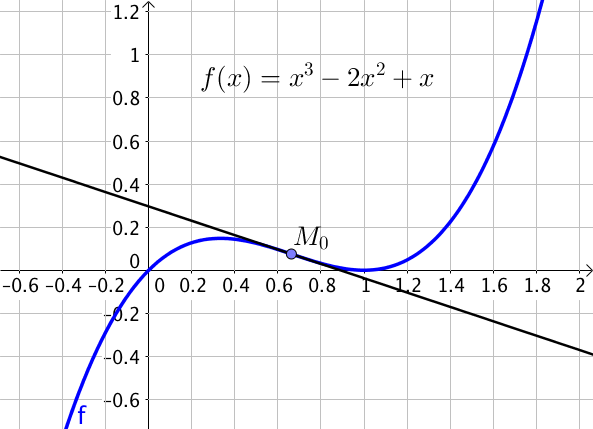
$f(x) = x^3 – 2x^2 + x$ pour tout réel $x$,
on cherche d’éventuels points d’inflexion.
Pour cela, on calcule tout d’abord $f’$ qui existe car $f$ est polynomiale.
Pour tout $x \in \mathbb{R}, \ f'(x) = 3x^2 – 4x + 1$.
De même, $f’$ est dérivable sur $\mathbb{R}$ car c’est une fonction polynomiale : $f”$ existe donc et
$f”(x) = 6x – 4$.
Pour trouver un point d’inflexion, on cherche à présent une valeur de $x$ pour laquelle la dérivée seconde s’annule et change de signe.
Soit $x \in \mathbb{R}, \ f”(x) = 0 \iff 6x – 4 = 0 \iff x = \dfrac{4}{6} \iff x = \dfrac{2}{3}$.
La dérivée s’annule donc en $x = \dfrac{2}{3}$.
On dresse alors le tableau de signe de $f”(x)$ pour tout réel $x$.
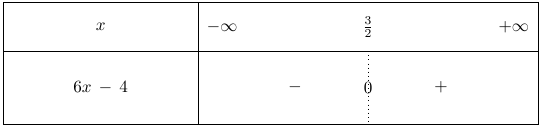
Ainsi, la dérivée seconde s’annule et change de signe en $x = \dfrac{2}{3}$.
Ainsi, $f$ admet un point d’inflexion en $x = \dfrac{2}{3}$.