Méthode des moindres carrés
Méthode des moindres carrés
Dans certains cas, le nuage de points d’une série statistique présente une trajectoire rectiligne, c’est à dire que les points semblent former une droite.
L’objectif de la méthode des moindres carrés est de déterminer une droite qui passe au plus près de chaque point afin de pouvoir approximer les valeurs inconnues de la série statistique.
On étudie la méthode à l’aide d’un exemple, qui correspond à une étude entre le nombre de buts marqués et le salaire annuel en millions d’euros de joueurs de L1.
| Nombre de buts | 2 | 8 | 11 | 16 | 20 |
| Salaire annuel en millions | 3,5 | 4,7 | 5,2 | 7,6 | 9,5 |
La méthode se calcule à l’aide de la calculatrice et permet d’obtenir la droite de régression linéaire.
La calculatrice permet d’obtenir l’équation de la droite de régression linéaire :
$y \approx 0,34x + 2,26$, qui passe au plus près des points.
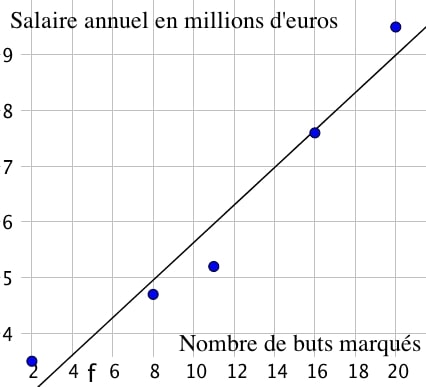
Si un attaquant marque 25 buts, d’après ce modèle il pourra prétendre à un salaire de $0,34\times 25 + 2.26 = 10.76$ millions d’euros.
Lors de la régression linéaire, la calculatrice affiche un coefficient $r$ qui vaut dans l’exemple $r \approx 0.97$.
Définition :
Le coefficient de corrélation noté $r$ est un nombre compris entre $-1$ et $1$ qui mesure la relation entre les variables $x$ et $y$.
Plus $r$ est proche de $-1$ ou $1$ plus la corrélation linéaire entre les variables est forte, c’est à dire plus l’approximation de la série statistique par une droite est pertinente.
Exemple
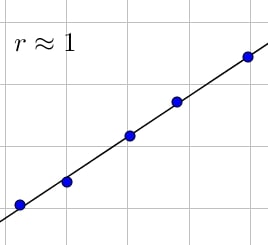
Dans ce cas, la droite de régression linéaire passe par tous les points et la droite est croissante car $r$ est positif.
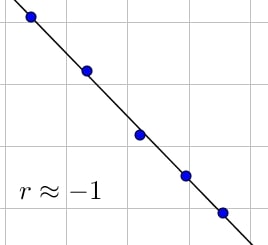
Dans ce cas, la droite de régression linéaire passe par tous les points et la droite est décroissante car $r$ est négatif.
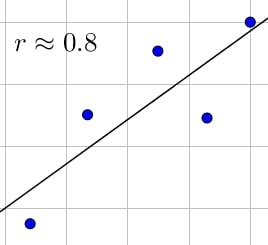
Dans ce cas les points sont plus éparses.
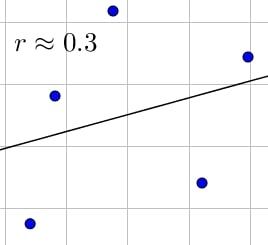
Dans ce cas là, la régression linéaire n’est plus pertinente.


