- 1Chute d'un objet avec vitesse - Étape 1 : Bien définir les conditions initiales
- 2Chute d'un objet avec vitesse - Étape 2 : Les coordonnées des vecteurs accélération et vitesse
- 3Chute d'un objet avec vitesse - Étape 3 : Les coordonnées du vecteur position
- 4Chute d'un objet avec vitesse - Étape 4 : L'équation de la trajectoire du mouvement
Chute d'un objet avec vitesse - Étape 1 : Bien définir les conditions initiales
Étape 1 : bien définir les conditions initiales
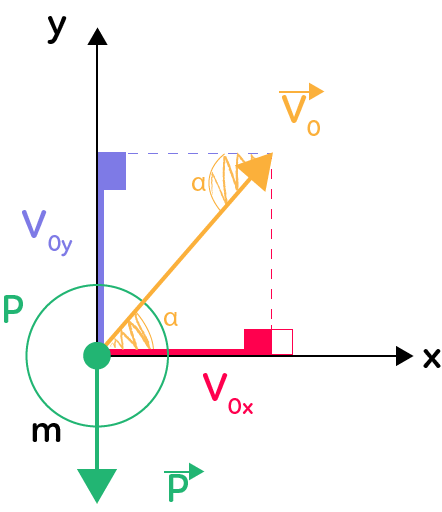
On étudie ici la mouvement d’une balle lancée depuis l’origine du repère avec une vitesse initiale représentée sur le schéma ci-contre par le vecteur $\overrightarrow{V_0}$.
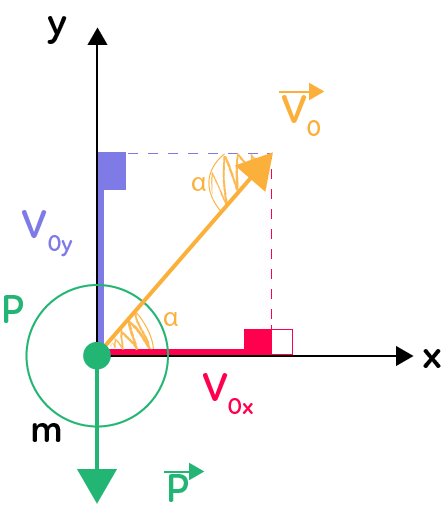
Il s’agit donc de déterminer les coordonnées du vecteur vitesse initiale, qui sont obtenues à partir de la projection du vecteur $\overrightarrow{V_0}$ sur les deux axes du repère. Le projeté du vecteur sur un axe est le segment délimité par l’origine du repère et l’intersection entre cet axe et la droite perpendiculaire à ce dernier passant par l’extrémité du vecteur. Le projeté selon $Ox$ est représenté en rouge et est noté $V_{Ox}$ : c’est la coordonnée selon $x$ du vecteur $\overrightarrow{V_0}$.
En outre, le vecteur vitesse initiale est incliné d’un angle $\alpha$ par rapport à l’axe des abscisses.
En utilisant les formules de trigonométrie, on trouve que $\cos(\alpha) = \dfrac{V_{Ox}}{ \|\overrightarrow{V_0} \|}$ et $\sin(\alpha) = \dfrac{V_{Oy}}{ \|\overrightarrow{V_0} \|}$. On vient ainsi de déterminer le vecteur vitesse initiale :
$\overrightarrow{V_0} \left\{
\begin{array}{ccc}
V_{Ox} & = & V_0 \times \cos(\alpha) \\
V_{Oy} & = & V_0 \times \sin(\alpha) \\
\end{array}
\right.$, où $V_0$ est la norme du vecteur vitesse initiale.
Le système d’étude est la balle, on se place dans le référentiel terrestre supposé galiléen (permettant ainsi d’utiliser les lois de Newton et en particulier la seconde loi).
La seule force agissant sur la balle est son poids, vertical descendant tel que $\overrightarrow{P} = m \times \overrightarrow{g}$.
D’après la deuxième loi de Newton, on peut écrire :
$\sum \overrightarrow{F_{ext}} = m \times \overrightarrow{a} $
D’après le bilan des forces, la somme des forces extérieures est équivalente au poids, ainsi :
$\overrightarrow{P} = m \times \overrightarrow{a} $ ou encore $m \times \overrightarrow{g} = m \times \overrightarrow{a} $.
On trouve donc $\overrightarrow{g} = \overrightarrow{a}$.
Chute d'un objet avec vitesse - Étape 2 : Les coordonnées des vecteurs accélération et vitesse
Étape 2 : les coordonnées des vecteurs accélération et vitesse
L’application de la seconde loi de Newton conduit à $\overrightarrow{a} = \overrightarrow{g}$, que l’on réécrit à l’aide des coordonnées des deux vecteurs : $ \left\{
\begin{array}{ccc}
a_x & = & 0 \\
a_y & = & -g \\
\end{array}
\right.$
Pour déterminer le vecteur vitesse, il faut se servir de la relation l’unissant à l’accélération : $\overrightarrow{a} = \dfrac{\text{d}\overrightarrow{v}}{\text{dt}}$. Il s’agit donc de trouver des primitives des coordonnées du vecteur accélération.
On obtient alors $\overrightarrow{v} \left\{
\begin{array}{ccc}
v_x & = & C_1 \\
v_y & = & -gt + C_2 \\
\end{array}
\right.$
On se sert alors des conditions initiales afin de déterminer la valeur des constantes en les identifiant.
A $t = 0$, on a ainsi :
$\overrightarrow{v} \left\{
\begin{array}{ccccc}
v_x & = & C_1 & = & v_0 \times \cos(\alpha) \\
v_y & = & -g\times 0 + C_2 & = & v_0 \times \sin(\alpha) \\
\end{array}
\right.$
Ayant ainsi trouvé la valeur des constantes, il est maintenant possible de déterminer entièrement la vitesse à tout instant :
$\overrightarrow{v} \left\{
\begin{array}{ccc}
v_x & = & v_0 \times \cos(\alpha) \\
v_y & = & -gt + v_0 \times \sin(\alpha) \\
\end{array}
\right.$
Afin de connaitre la valeur de la vitesse à chaque instant, il faut calculer la norme du vecteur vitesse, définie par : $\|\overrightarrow{v}\| = \sqrt{v_x^2 + v_y^2}$.
Chute d'un objet avec vitesse - Étape 3 : Les coordonnées du vecteur position
Étape 3 : Les coordonnées du vecteur position
En primitivant les coordonnées du vecteur accélération et à l’aide des conditions initiales, on a pu obtenir l’expression des coordonnées du vecteur vitesse $\overrightarrow{v} \left\{
\begin{array}{ccc}
v_x & = & v_0 \times \cos(\alpha) \\
v_y & = & -gt + v_0 \times \sin(\alpha) \\
\end{array}
\right.$
Afin de connaître le mouvement de la balle à chaque instant, il s’agit à présent de déterminer le vecteur position, relié au vecteur vitesse par la relation : $\overrightarrow{v} = \dfrac{\text{d}\overrightarrow{OG}}{\text{dt}}$ ou en d’autres termes le vecteur vitesse est la dérivée par rapport au temps du vecteur position.
Pour obtenir les coordonnées du vecteur position, il faut trouver des fonctions dont la dérivée est égale aux coordonnées du vecteur vitesse : ce sont les primitives des coordonnées du vecteur vitesse.
Ainsi, $\overrightarrow{OG} \left\{
\begin{array}{ccc}
x & = & v_0 \times \cos(\alpha)\times t + C_3 \\
y & = & -\dfrac{1}{2} \times gt^2 + v_0 \times \sin(\alpha) \times t + C_4 \\
\end{array}
\right.$
Il ne faut pas oublier d’ajouter une constante lorsque l’on primitive une fonction, que l’on détermine en utilisant les conditions initiales.
Or à $t = 0$, la balle est lancée depuis l’origine du repère, on a donc $\overrightarrow{OG} = \overrightarrow{0}$ et par identification, en remplaçant $t$ par 0 :
$\overrightarrow{OG} \left\{
\begin{array}{ccccccc}
x & = & v_0 \times \cos(\alpha)\times 0 + C_3 &=& C_3 &=& 0 \\
y & = & -\dfrac{1}{2} \times g \times 0^2 + v_0 \times \sin(\alpha) \times 0 + C_4 &=& C_4 &=& 0 \\
\end{array}
\right.$
Ainsi, on peut réécrire le vecteur position quelque soit l’instant :
$\overrightarrow{OG} \left\{
\begin{array}{ccc}
x & = & v_0 \times \cos(\alpha)\times t \\
y & = & -\dfrac{1}{2} \times gt^2 + v_0 \times \sin(\alpha) \times t \\
\end{array}
\right.$
Ce système d’équation est appelé les équations horaires de la balle.
Chute d'un objet avec vitesse - Étape 4 : L'équation de la trajectoire du mouvement
Étape 4 : l’équation de la trajectoire d’un mouvement
Les équations horaires ont été déterminées : $\overrightarrow{OG} \left\{
\begin{array}{ccc}
x & = & v_0 \times \cos(\alpha)\times t \\
y & = & -\dfrac{1}{2} \times gt^2 + v_0 \times \sin(\alpha) \times t \\
\end{array}
\right.$
Il est désormais possible d’établir l’équation de la trajectoire, permettant de suivre le trajet de la balle, et s’écrivant de la forme $y = f(x)$, où $f$ est la fonction indépendante du temps qu’il faut déterminer.
Afin d’éliminer le temps au profit des autres paramètres $x$ et $y$, on détermine la valeur de $t$ en fonction de $x$ : $t = \dfrac{x}{v_0\times \cos(\alpha)}$.
On remplace ensuite cette nouvelle valeur de $t$ dans l’expression de $y$ :
$y = -\dfrac{1}{2} \times g \times \left( \dfrac{x}{v_0\times \cos(\alpha)} \right)^2 + v_0 \times \sin(\alpha) \times \dfrac{x}{v_0\times \cos(\alpha)}$
On simplifie alors et distingue les constantes de la variable $x$ :
$y = -\dfrac{g}{2v_0^2\cos(\alpha)^2} \times x^2 +\tan(\alpha) \times x$
C’est l’équation de la trajectoire, on peut associer une coordonnée $x$ à la coordonnée $y$ correspondante à un temps défini. En outre, il s’agit de l’équation d’une parabole, qui dépend de l’angle avec lequel la balle a été lancée initialement.


