Mouvement dans un champ de pesanteur uniforme : équations horaires
Mouvement dans un champ de pesanteur uniforme : équations horaires
Dans un champ de pesanteur uniforme, “uniforme” veut dire que l’on parle du même vecteur $\overrightarrow{g}$ en tout point de l’espace. Typiquement, si l’on se trouve non loin de la surface de la Terre, on considère que $\overrightarrow{g}$ est uniforme donc le champ de pesanteur l’est aussi.
I. Situation
Si l’on prend un repère $(O,x,y,z),$ il faut qu’il soit orthonormé direct, c’est-à-dire que $x, y$ et $z$ forme un trièdre. Le point au centre du cercle montre que le $z$ se dirige vers nous. Ensuite, nous retrouvons un point $M$ d’abscisse $0$ et d’ordonnée $h,$ ce qui veut dire que le mobile n’est pas tout à fait au niveau du sol au moment de sa situation initiale. Ce point $M$ aura aussi une vitesse initiale $v_0$ qui aura un angle $\alpha$ avec l’horizontale. Ceci est donc notre situation de départ.
On observe alors deux grandes situations :
– Si $v_0$ est égal au vecteur nul, cela veut dire qu’on lâche l’objet sans vitesse initiale. On appelle ça la chute libre. Le mouvement sera alors vertical.
– Si $v_0$ est différent du vecteur nul, cela veut dire que l’on donne une impulsion au départ à notre objet. On aura alors une trajectoire parabolique.
II. Les conditions initiales
Dans un exercice, il est intéressant de développer tout de suite les vecteurs (tel que $\overrightarrow{v}_0$ par exemple) en les projetant sur les différents axes au brouillon.
À quoi la vitesse initiale $ \overrightarrow{v}(t=0)$ (donc au temps 0) est-elle égale ? Pour répondre à cette question, nous allons nous aider d’un schéma.
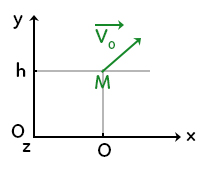
Dans ce repère, on reproduit donc le vecteur $\overrightarrow{v}_0$ en plaçant l’angle $\alpha$. Le reste n’est que de la trigonométrie. Pour avoir la projection horizontale on va utiliser cos. On obtiendra donc la longueur égale à $ v_0 \cos(\alpha)$. Et pour avoir la projection sur l’axe $y,$ cela sera égal à $ v_0 \sin(\alpha).$
Ainsi $ \overrightarrow{v}(t=0) =\begin{pmatrix} v_0 \cos(\alpha) \\ v_0 \sin(\alpha) \\ 0 \end{pmatrix} $
Sur l’axe des $z,$ il n’y a pas de vitesse initiale, c’est pourquoi $Uz$ est égal a $0.$
La position initiale est égale a : $\overrightarrow{OM}(t=0) = \begin{pmatrix} 0 \\ h \\ 0 \end{pmatrix}$
III. Calcul de la vitesse
Pour rappel, l’accélération est la dérivée de la vitesse par rapport au temps ( $\overrightarrow{a} = \dfrac{d \overrightarrow{v}}{d\overrightarrow{t}}$). La vitesse $\overrightarrow{v}$ est alors la primitive de l’accélération. Le système étudié ici est l’objet de masse $m. $ On suppose que l’on se trouve dans un référentiel galiléen, ce qui implique la deuxième loi de Newton :
$\sum \overrightarrow{F_{ext}} = m \times \overrightarrow{a} = m \overrightarrow{g} $ car la seule force ici est le poids $mg.$ On peut donc simplifier par $m$ et on se retrouve avec $\overrightarrow{a} = \overrightarrow{g}.$
Si l’on projette l’accélération vectorielle sur les trois axes $x, y$ et $z,$ on se retrouve avec :
$\begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}$
et pour $g$ : $ \begin{pmatrix} 0 \\ -g \\ 0 \end{pmatrix} $
On a donc $\begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} = \begin{pmatrix} 0 \\ -g \\ 0 \end{pmatrix} $
On sait que pour trouver la vitesse, il faut faire la primitive. On a donc :
$\begin{pmatrix} v_x = constante \\ v_y= -gt + constante’ \\ v_z = constante” \end{pmatrix}$
Pour trouver les constantes, il faut toujours partir des conditions initiales (CI). Ainsi on a :
$V_x(t=0) = v_0 \cos(\alpha)$ = constante
$V_y(t=0) = v_0 \sin(\alpha)$ = constante’
$V_z(t=0) = 0 = constante”$
Au final, on a donc $ \begin{pmatrix} v_x(t) = v_0 \cos(\alpha) \\ v_y(t) = -gt + v_0 \sin(\alpha) \\ v_z(t) = 0 \end{pmatrix}$
IV. Calcul de la position en fonction du temps
Pour rappel : $\overrightarrow{v} = \dfrac{d\overrightarrow{OM}}{dt},$ ainsi la position est la primitive de la vitesse. Nous avons aussi calculé la vitesse $\overrightarrow{v} = \begin{pmatrix} v_0\cos(\alpha) \\ -gt + v_0\sin(\alpha) \\ 0 \end{pmatrix} $
Il suffit de primitiver. On a alors :
$\overrightarrow{OM} = \begin{pmatrix} v_0\cos(\alpha) \times t + constante \\ – \dfrac{1}{2}gt^2 + v_0\sin(\alpha) \times t+ constante’ \\ constante” \end{pmatrix} $
Ne SURTOUT PAS oublier les constantes. Comme vu précédemment, nous allons encore une fois nous aider des conditions initiales :
$\overrightarrow{OM} (t=0) = \begin{pmatrix} 0 = constante \\ h = constante’ \\ 0 = constante” \end{pmatrix} $
Si on remplace dans notre expression avec les nouvelles constantes trouvées, on a :
$\overrightarrow{OM} (t) = \begin{pmatrix} v_0\cos(\alpha) \times t \\ – \dfrac{1}{2}gt^2 + v_0\sin(\alpha) \times t+ h \\ 0 \end{pmatrix} $
Ainsi ce que nous venons de voir est bien l’accélération en fonction du temps, la vitesse en fonction du temps et la position en fonction du temps, d’où les équations horaires. La coordonnée sur l’axe $ z$ est égale à $0,$ d’où le fait qu’elle ne varie pas en fonction du temps. C’est un mouvement « plan », la coordonnée de la position ne varie que dans la direction de l’axe $x$ ou $y.$
Mouvement dans un champ de pesanteur uniforme : étude de la trajectoire
I. Equation de la trajectoire
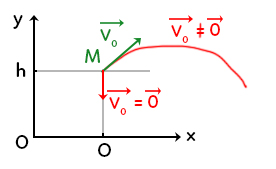
Sur ce schéma, nous avons un point $M$ d’abscisse $0$ et d’altitude $h.$ L’axe $z$ n’est pas représenté car nous savons déjà que le point reste toujours dans la direction $z=0.$
Il y a deux situations :
– Si la vitesse initiale est différente de zéro, c’est un mouvement parabolique.
– Si la vitesse initiale est égale au vecteur nul, c’est une chute libre.
Pour rappel, ce qui a été vu dans les équations horaires : l’expression du vecteur position $ \overrightarrow{OM}(t) = \begin{bmatrix} v_0 \times \cos(\alpha)\times t \\ -\dfrac{1}{2}\times g \times t^2+ v_0 \times \sin(\alpha)\times t+h \end{bmatrix}$
Dans un premier temps, nous allons isoler le temps (t) grâce à l’équation 1. Ainsi on a :
$X(t) = v_0\times \cos(\alpha)\times t $ -> $t = \dfrac{x(t)}{ v_0\times \cos(\alpha) }$
Cela est vrai si $v_0$ est différent de zéro, sinon nous sommes dans une forme indéterminée (division par zéro).
Maintenant que nous avons l’expression de $t,$ nous « l’injectons » dans l’équation 2. Ainsi on a :
$Y(t) = -\dfrac{1}{2}\times g\times \dfrac{x}{ v_0\times \cos(\alpha) }^2+ v_0\times \sin(\alpha) \times \dfrac{x}{ v_0 \times \cos(\alpha)}+h $
On commence à voir se dessiner l’équation paramétrique. C’est-à-dire $y$ en fonction de $x,$ car la variable $t$ a disparue au profit de la variable $x.$
$Y(t) = -\dfrac{g}{2 v_0^2\times \cos^2(\alpha)}\times x^2+ \tan(\alpha)\times x+h $
Les $v_0$ se simplifient et sin/cos donne tangente. Tout cela n’est vrai que si $v_0$ est différents de zéro. Nous avons alors trouvé l’équation d’une parabole (de type $ax^2+bx+c$).
Que se passe-t-il si $v_0$ est égal à zéro ?
il faut revenir au moment où cela pose problème pour la première fois, c’est-à-dire au moment de l’équation $X(t) = v_0 \times \cos(\alpha)\times t $ -> $t = \dfrac{x(t)}{ v_0\times \cos(\alpha) }$
Ainsi si $v_0$ vaut zéro, $x(t) = 0$ (effectivement lors d’une chute verticale on reste toujours avec une abscisse égale à zéro).
Alors pour la deuxième équation, nous aurons $y(t) = -\dfrac{1}{2} \times g \times t^2 + h $
Nous retrouvons bien l’équation d’un objet qui chute verticalement.
II. La portée et la flèche
On retrouve souvent ce genre de question dans les exercices, par exemple calculer la portée d’un tir. C’est-à-dire la hauteur atteinte par un ballon qu’on a lancé. Dans chaque cas, il faut savoir quel est le point de départ pour pouvoir calculer.
Qu’est-ce que la portée ?
C’est la distance que l’objet a parcouru entre sa position de départ et sa position finale, c’est-à-dire quand il touche le sol. Ainsi l’objet est partit à une certaine abscisse et arrive à une certaine abscisse et la distance entre les deux abscisses est la portée.
Pour rechercher la portée : la condition est de se trouver au sol, c’est-à-dire que l’altitude vaut zéro. Soit $y(x) = 0.$
Il faudra par la suite résoudre cette équation. En la résolvant, nous allons trouver une expression de $x, $et celle-ci sera alors l’abscisse à laquelle l’objet a touché le sol. Ce sera donc la portée.
Qu’est-ce que la flèche ?
C’est la hauteur maximale que va atteindre le système mécanique.
Pour rechercher la flèche : comment savoir quelle est l’altitude maximale atteinte lors de la trajectoire parabolique ?
Au sommet nous somme au maximum de la fonction $y = f(x),$ et quand on atteint un maximum, sa dérivée est nulle.
Ainsi $\dfrac{dy}{dx} = 0 $
C’est cela que nous allons exploiter et qu’il faudra alors résoudre. Cela va nous donner une solution qui sera la réponse à la question « quelle est la flèche ? »
III. La norme de la vitesse
Pour rappel : $ \| vec v \| = \sqrt{V_x^2+V_y^2+v_z^2} $
$= (v_0^2 cos^2(\alpha) + g^2 t^2 + v_0^2 sin^2 (\alpha) – 2 g t v_0 sin(\alpha))^{\frac{1}{2}}$ or la somme de $cos^2 (\alpha) $ et $sin^2 (\alpha) $ donne $1$
$=[v_0^2 +gt (gt- 2v_0 sin(\alpha))]^{\frac{1}{2}}$
Cette expression sert notamment dans les exercices où l’on peut poser des questions comme l’énergie cinétique. Celle-ci est égale à ½ de la masse du système multipliée par la vitesse au carré. La vitesse dont on parle est la norme, ici ce serait donc celle calculée au-dessus.
Calcul de la portée
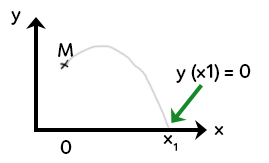
Sur le schéma ci-dessus, on voit la trajectoire parabolique et l’équation de $y$ au point d’impact au niveau du sol ($y(x1) = 0$).
Ainsi on a :
$y(t) = -\dfrac{g}{2 v_0^2 \times \cos^2(\alpha)} \times x1^2+ \tan(\alpha) \times x1+h = 0$
C’est une équation du second degré.
On va d’abord calculer le discriminant :
$ \Delta = \tan^2(\alpha) + \dfrac{2g}{ v_0^2 \times \cos^2(\alpha)}*\times h$ $ (> \tan^2(\alpha)$
On additionne une tangente au carré et un nombre qui est toujours positif, d’où :
$x_{1,1} = \dfrac{-\tan(\alpha)-\sqrt{\Delta}}{\dfrac{-g}{ v_0^2 \times \cos^2(\alpha)}} =\dfrac{\tan(\alpha)+\sqrt{\Delta}}{g}\times v_0^2\times\cos^2(\alpha)$
$ x_{121} = \dfrac{-\tan(\alpha)+\sqrt{\Delta}}{\dfrac{-g}{ v_0^2 \times \cos^2(\alpha)}} =\dfrac{\tan(\alpha)-\sqrt{\Delta}}{g}\times v_0^2\times \cos^2(\alpha) $
Ici on se retrouverait avec $< 0,$ donc une abscisse dans les négatifs. Or ce n’est pas possible car nous sommes partis de l’abscisse zéro. On peut donc éliminer la deuxième solution.
Il ne nous reste alors plus que la première solution. Ainsi la portée sera égale à l’abscisse $x1,1$ : c’est-à-dire à la portée = $x1,1.$
Calcul de la flèche
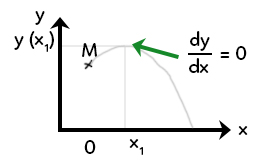
On veut savoir quelle est l’altitude maximale atteinte. Au point maximal, la dérivée $\dfrac{dy}{dx} = 0 $
Donc on résout $-\dfrac{g }{ v_0^2\times \cos^2(\alpha)}\times x1+ \tan(\alpha) = 0 $
D’où $x1 = \tan(\alpha)\times \dfrac{ v_0^2\times \cos^2(\alpha) }{g} $
Il faut alors trouver l’altitude, d’où la flèche $= y(x1),$ d’où :
$=-\dfrac{g }{ 2\times v_0^2\times \cos^2(\alpha)}\times \tan^2(\alpha)\times \dfrac{ v_0^4\times \cos^4(\alpha) }{ g^2} +\tan^2(\alpha) \times \dfrac{ v_0^2\times \cos^2(\alpha) }{ g}+h $
$= \dfrac{ v_0^2\times \sin^2(\alpha) }{g}\times (1- \dfrac{1}{2})+h$
$= \dfrac{ v_0^2\times \sin^2(\alpha) }{ 2g}+h$


