- 1Mouvement d'un satellite autour d'une planète - Étape 1 : Système, référentiel et bilan des forces
- 2Mouvement d'un satellite autour d'une planète - Étape 2 : La deuxième loi de Newton
- 3Mouvement d'un satellite autour d'une planète - Étape 3 : La vitesse du satellite
- 4Mouvement d'un satellite autour d'une planète - Étape 4 : La période de révolution
Mouvement d'un satellite autour d'une planète - Étape 1 : Système, référentiel et bilan des forces
Étape 1 : Système, référentiel et bilan des forces
L’étude du mouvement d’un satellite autour d’une planète peut se transposer à l’étude de tout corps en mouvement autour d’un autre corps.
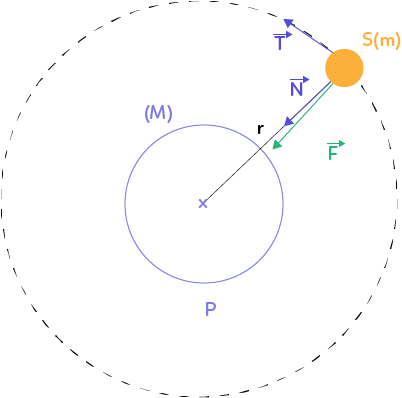
On considère une planète quelconque notée $P$ de masse $M$ et un satellite en mouvement circulaire autour de celle-ci noté $S$ de masse $m$.
Avant de débuter l’étude, il s’agit de définir les vecteurs car les forces sont représentées par des vecteurs.
Les pointillés symbolisent la trajectoire du satellite, dans l’approximation des trajectoires circulaires. On place ensuite sur ce trajet deux vecteurs, un vecteur tangentiel à la trajectoire $\overrightarrow{T}$ et un vecteur normal (perpendiculaire) à la trajectoire $\overrightarrow{N}$. C’est le repère de Frenet.
On détermine et énonce dans un premier temps le système d’étude $S$. Il s’agit ici du satellite.
On définit ensuite le référentiel d’étude muni d’une base de temps et d’un repère (les deux vecteurs). Le référentiel utilisé ici est le centre de la planète muni de trois axes dirigés vers trois étoiles lointaines, permettant ainsi d’avoir un référentiel fixe par rapport à la durée de l’expérience : il s’agit ainsi d’un référentiel supposé galiléen, où l’on peut appliquer les lois de Newton.
On détermine ensuite les actions auxquelles est soumis le satellite : c’est le bilan des forces.
Il s’agit ici de la force d’interaction gravitationnelle entre la planète et le satellite notée $\overrightarrow{F_G}$.
D’après la loi des actions réciproques (ou 3e loi de Newton), si un objet A subit une action d’un objet B, alors l’objet B subit la même action de l’objet A.
Cependant, il ne faut pas représenter les deux forces. L’objet d’étude est uniquement le satellite, il s’agira donc de représenter uniquement les forces agissant sur le satellite.
Mouvement d'un satellite autour d'une planète - Étape 2 : La deuxième loi de Newton
Étape 2 : La deuxième loi de Newton
Le référentiel est galiléen, permettant ainsi d’appliquer les lois de Newton, et en particulier la seconde loi de Newton.
Cette dernière stipule que :
$\sum \overrightarrow{F_{ext}} = m \times \overrightarrow{a_{satellite}} = \dfrac{\text{d}\overrightarrow{p}}{\text{dt}}$,
ou encore que la somme des forces extérieures agissant sur le satellite est égale au produit de la masse du satellite par l’accélération de ce dernier ou à la dérivée de la quantité de mouvement du satellite par rapport au temps.
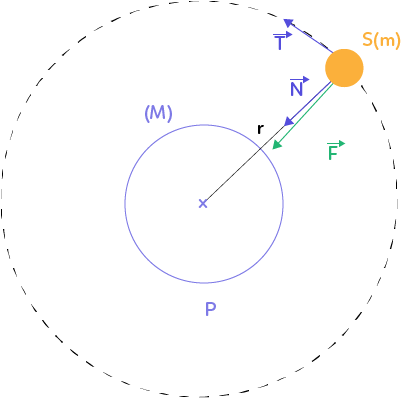
Ici, la seule force que subit le satellite est la force d’interaction gravitationnelle. Cette force est dirigée par la droite reliant les centres du satellite et de la planète et orientée du satellite vers la planète. La distance entre les deux centres est notée $r$.
Ainsi on trouve $\overrightarrow{F_G} = m \times \overrightarrow{a}$ que l’on peut réécrire dans la base $\left (\overrightarrow{T}, \overrightarrow{N} \right)$ en utilisant la formule de la force d’attraction gravitationnelle sous la forme :
$ G \times \dfrac{M \times m}{r^2} \times \overrightarrow{N} = m \times \overrightarrow{a}$ où $G$ est la constante universelle de gravitation, $\overrightarrow{N}$ est un vecteur unitaire qui donne uniquement l’orientation de la force, $M$ la masse la planète qui agit et $m$ la masse du satellite. On prêtera une attention particulière à écrire une relation vectorielle, c’est-à-dire ici à ne pas oublier $\overrightarrow{N}$ .
On parvient ainsi à la relation vectorielle de l’accélération :
$ \overrightarrow{a} = G \times \dfrac{M}{r^2} \times \overrightarrow{N}$
Ainsi le vecteur accélération est orienté selon $\overrightarrow{N}$, il n’y a donc pas d’accélération selon la composante tangentielle $\overrightarrow{T}$.
Mouvement d'un satellite autour d'une planète - Étape 3 : La vitesse du satellite
Étape 3 : la vitesse du satellite
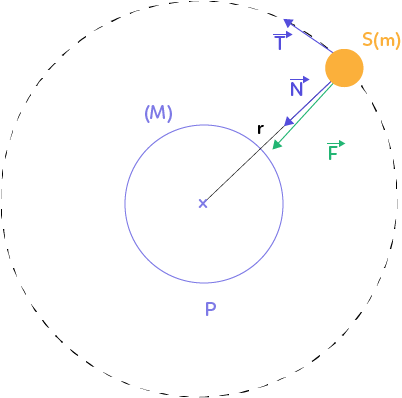
L’application de la seconde loi de Newton au satellite a permis de trouver la relation vectorielle suivante :
$\overrightarrow{a} = \dfrac{G M}{r^2} \overrightarrow{N}$ où $G$ est la constante universelle de gravitation, $M$ la masse de la planète, $r$ la distance séparant les centres du satellite et de la planète et $\overrightarrow{N}$ est un vecteur unitaire normal à la trajectoire.
En supposant le mouvement du satellite circulaire, on peut réécrire la formule du vecteur accélération : $\overrightarrow{a} = a_t \overrightarrow{T} + a_n \overrightarrow{N}$.
De plus, pour un mouvement circulaire, on dispose également de la relation suivante :
$\overrightarrow{a} = \dfrac{\text{d}v}{\text{dt}}\overrightarrow{T} + \dfrac{v^2}{r} \overrightarrow{N}$ où $v = \| \overrightarrow{v} \|$ et $\overrightarrow{v}$ est le vecteur vitesse du satellite.
En combinant les différents résultats, on obtient :
$ \dfrac{G M}{r^2} \overrightarrow{N} = \dfrac{\text{d}v}{\text{dt}}\overrightarrow{T} + \dfrac{v^2}{r} \overrightarrow{N}$.
Cela signifie dans un premier temps que, l’accélération étant uniquement portée par $\overrightarrow{N}$, le terme devant $\overrightarrow{T}$ est nul. En d’autres termes, cela signifie que $ \dfrac{\text{d}v}{\text{dt}} = 0$ ou encore que la vitesse du satellite est une constante : le mouvement du satellite est donc un mouvement circulaire uniforme.
Mais on peut aussi dans un second temps en déduire que $\dfrac{v^2}{r} = \dfrac{GM}{r^2}$ car ces deux termes sont tous deux portés par le vecteur normal $\overrightarrow{N}$. On en déduit finalement que $v = \sqrt{\dfrac{GM}{r}}$.
Mouvement d'un satellite autour d'une planète - Étape 4 : La période de révolution
Étape 4 : la période de révolution
On dispose, après calculs, de l’expression de la vitesse : $v = \sqrt{\dfrac{GM}{r}}$.
On souhaite déterminer la période de révolution $T$ du satellite, c’est-à-dire le temps qu’il met pour parcourir l’intégralité de son orbite autour de la planète.
Pour se faire, on sait que la vitesse est égale au rapport entre la distance parcourue et la durée nécessaire pour la parcourir ou encore $v = \dfrac{d}{\Delta t}$.
La distance parcourue correspond à la circonférence du cercle sur lequel se trouve le satellite alors que la durée correspond par définition à la période de révolution.
Ainsi, on peut réécrire la formule précédente : $v = \dfrac{2\pi r}{T}$.
On peut à présent utiliser l’expression de la vitesse obtenue après calculs pour parvenir à l’égalité suivante :
$ \sqrt{\dfrac{GM}{r}} = \dfrac{2\pi r}{T} $ que l’on peut élever au carré pour se débarrasser de la racine : $ \dfrac{GM}{r} = \dfrac{4 \pi ^2 r^2}{T^2}$ puis on isole la période de révolution : $T^2 = \dfrac{4 \pi^2 r^3}{GM}$.
La distance entre les deux centres dépendant du satellite, on regroupe alors les termes propres au satellite et les termes constants ($G$, $M$, $4 \pi^2$) : $\dfrac{T^2}{r^3} = \dfrac{4 \pi^2}{GM}$, où $T$ est en seconde, $r$ en mètre et $M$ en kilogramme.
On vient de démontrer la troisième loi de Kepler, stipulant que le rapport entre le carré de la période de révolution d’une satellite par le cube de la distance entre les centres du satellite et de la planète est une constante. Ainsi, si la planète possède plusieurs satellites sur des orbites différents ayant ainsi des périodes de révolution différentes, le rapport précédent sera toujours constant, pour n’importe quel satellite. On pourrait donc calculer la masse de la planète ou la période de révolution d’un autre satellite.
L’étude menée précédemment peut se généraliser à l’étude du mouvement de tout corps orbitant autour d’un autre, en particulier à celle des planètes autour du Soleil.
L’étude consistera tout d’abord à montrer que le mouvement est uniforme dans l’approximation circulaire, de trouver l’expression de la vitesse puis celle de la période de révolution.


