Système dans un champ électrique, accélérateur linéaire de particules
Système dans un champ électrique
L’objectif est de trouver l’équation de la trajectoire de ce système. Le système mécanique est une particule de charge $q$ et de masse $m.$ Si la particule n’a pas de charge, elle ne subira pas de champ électrique.
Exemple d’un champ électrique vers le bas. Pour les vecteurs unitaires, la norme du vecteur vaut 1. A t =0, la particule est à une altitude $h$ et une vitesse $v0$ selon l’axe $x.$
$\overrightarrow{E} = -E e\overrightarrow{y}$.
Le terme $-E$ correspond à la projection du vecteur $E$ sur $\overrightarrow{y}$. Ici, on est dans le cas où l’on suppose que $E$ est positif.
I. Deuxième loi de Newton
On suppose qu’on se trouve dans un référentiel galiléen. La somme des forces vaut la masse multipliée par l’accélération : $\overrightarrow{P} + \overrightarrow{F_e} = m \times \overrightarrow{a}$.
On a donc le poids et la force électrique. On néglige le poids et on obtient : $\overrightarrow{F_e} = m \times \overrightarrow{a}$.
Parfois, on doit le démontrer et parfois on le pose comme une hypothèse.
II. Projection et intégrations
On projette l’équation vectorielle précédente sur ($\overrightarrow{u_x}$ ; $\overrightarrow{u_y}$) : la force électrique est vers le bas puisqu’elle est égale à la charge multipliée par le champ électrique. Elle est colinéaire à $E$ donc la projection sur l’axe horizontale vaut 0.
De plus, la projection de l’accélération sur l’axe horizontal est appelée $a_x.$ Par définition, l’accélération est la dérivée de la vitesse par rapport au temps donc $a_x =\dfrac{dv_x}{dt}$.
On projette maintenant sur l’axe vertical : la force électrique est égale à $q\times E$. La projection du champ électrique vaut $-E,$ donc on a : $-q\times E$.
La projection de l’accélération sur l’axe vertical est $a_y.$ $a_y = \dfrac{dv_y}{dt}$.
On intègre ensuite par rapport au temps : $cte = m\times v_x$. La primitive de la dérivée d’une fonction est égale à la fonction.
On intègre la deuxième ligne : $-qE\times t + cte’ = m \times v_y$. Il reste toujours une constante quand on intègre.
Pour déterminer les constantes, on utilise les conditions initiales. A t = 0 : $v_x = v_0$ et $v_y = 0$.
Or : $v_x = \dfrac{cte}{m}$ et $v_y = \dfrac{-qEt+cte}{m}$.
D’où, comme t = 0 : $cte = m\times v_0$ et $cte’ = 0$.
On intègre de nouveau par rapport au temps, on a alors : $mv_0t + cte = mx$.
Pour la deuxième équation, on a : $-\dfrac{1}{2}qEt^2+cte’ = my$.
La nouvelle constante prime est apparue suite à la deuxième intégration. La première constante prime est égale à 0. A t = 0, x = 0 et y = h. Donc la constante vaut 0 et la constante prime vaut $m$ multiplié par $h.$
Donc, les équations horaires sont $x = v_0t$ (2) et $y = h -\dfrac{qEt^2}{2m}$(3).
On dit équations horaires car $x$ et $y$ dépendent du temps.
On va isoler $t$ dans l’équation (2). On obtient $t = \dfrac{x}{v_0}$, qu’on va injecter dans (3). On substitue $t$ par sa valeur trouvée. On obtient alors : $y = h – \dfrac{qE}{2mv_0^2}\times x^2$.
On a alors l’équation de la trajectoire. Cela correspond à une équation polynomiale du second degré. Cela ressemble à une parabole (vu en mathématiques). La parabole peut monter ou descendre : cela va dépendre du signe de la fraction devant le x2. Lorsque x = 0, y = h. La parabole va monter quand le champ est vers le haut et descendre lorsqu’il est vers le bas. La direction du champ changera le signe de $E.$ On a défini au début que le champ $E $est positif lorsqu’il est dirigé vers le bas.
L'accélérateur linéaire de particules
L’objectif est de donner de la vitesse à des particules chargées, pour pouvoir par la suite, faire des études sur celles-ci.
I. Force électrique
Il existe une relation entre la force électrique $F$ et le champ électrique $E$ :
$\overrightarrow{F} = q \times \overrightarrow{E}$
$F$ étant la force électrique en Newton, $q$ la charge de la particule en Coulomb (C) et $E$ le champ électrique en V.m-1.
A champ électrique constant, plus la charge est grande plus la force électrique générée est grande. Pour résumer, grâce à un champ électrique $E,$ on a une mise en mouvement.
II. Création du champ électrique
On relit le côté positif du générateur à une plaque et le côté négatif à une autre plaque :
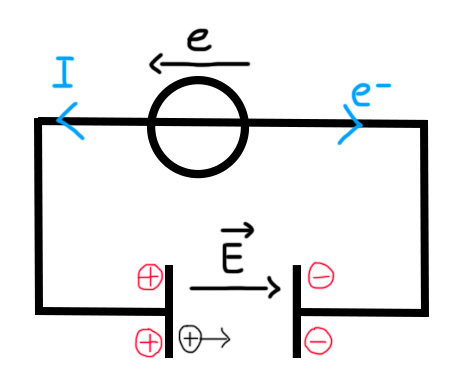
Dans ce type de montage, le courant circule au départ de la borne positive du générateur. Les électrons circulent en sens inverse. Les électrons vont arriver à la plaque mais derrière la plaque on a de l’air ou un isolant qui empêche les électrons de passer. Les charges négatives vont donc s’accumuler sur la plaque. Pour le courant, c’est la même chose : les charges positives vont s’accumuler sur la plaque de l’autre côté. Il manquera donc sur la plaque de droite des charges positives pour compenser et sur la plaque de gauche des charges négatives pour compenser.
A l’intérieur de ces deux plaques, un champ électrique va être créé. Il se dirige vers la droite. Pourquoi ?
Car si on lâche une charge positive à l’intérieur de cet espace, elle va être attirée par les charges négatives et repoussée par les charges positives, donc elle va se diriger vers la droite. Selon la formule, si la charge est positive, la force et le champ seront dans la même direction, donc vers la droite ici. On va vouloir utiliser pour la suite le théorème de l’énergie cinétique. Cela va faire intervenir le travail des forces.
III. Travail de la force électrique
Au niveau de la plaque de gauche on pose le point $A$ et au niveau de la plaque de droite le point $B.$ Entre les deux, on a vu qu’il y avait un champ électrique dirigé vers la droite.
Calculons le travail de la force qui va de $A$ vers $B.$
Le système sera : à l’état initial, une charge $q$ en $A$ et à l’état final, une charge $q$ en $B.$ Le travail c’est quoi ? Quand la force électrique est constante, on a :
$W_{A->B}(\overrightarrow{F}) = \overrightarrow{F}.\overrightarrow{AB}$.
On a alors : $W_{A->B}(\overrightarrow{F}) = q \overrightarrow{E} \overrightarrow{AB}$.
Les vecteurs sont tous les deux dans le même sens donc on aura : $W_{A->B}(\overrightarrow{F}) = qE\times AB = q\times U_{AB}$.
On vient donc de montrer que $W_{A->B}(\overrightarrow{F}) = q\times U_{AB}= V_A-V_B$.
Pour revenir à l’exemple du schéma précédent, on voit que la plaque de gauche est reliée à un fil, la plaque de droite également. Le potentiel à gauche est connecté à la borne positive du générateur et le potentiel de droite est connecté à la borne négative du générateur. Donc, $V_A-V_B$ correspond à $e$ : c’est la tension du générateur. $U_{AB}$ est la tension du générateur.
IV. Théorème de l’énergie cinétique
La variation d’énergie cinétique entre deux états est égale au travail entre $A$ et $B$ des forces : $\Delta E_c = W_{A->B}(\overrightarrow{F})$.
On n’a pas dressé de bilan des forces car on néglige le poids. Dans le cas des accélérateurs de particules, on peut montrer que le poids est négligeable devant la force électrique. Il n’apparaitra pas dans la formule et dans le travail des forces on n’aura que celui de la force électrique.
On a alors : $\dfrac{1}{2}mv_B^2-\dfrac{1}{2}mv_A^2 = q \times U_{AB}$.
Supposons que la particule n’a pas de vitesse à l’état initial : $vA = 0.$
On peut donc isoler vB : $v_B = \sqrt{\dfrac{2qU_{AB}}{m}}$.
On a donc réussi à donner de la vitesse à la particule puisqu’en $B,$ la particule aura une certaine vitesse liée à sa masse, à sa charge et à la tension entre les deux plaques. Plus la tension est importante, plus la vitesse en $B$ sera importante.
V. Exemple d’accélérateur
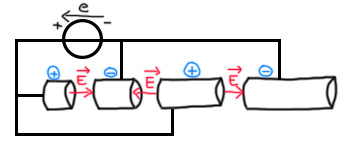
On a un générateur avec, comme tout à l’heure, une borne positive qui va vers la plaque chargée positivement et une borne négative qui va vers une plaque chargée négativement. Ici, Côté positif, on va être relié à un cylindre creux chargé positivement, suivi d’un deuxième cylindre creux chargé négativement (car relié à la borne négative du générateur). Entre ces deux cylindres, on a un espace avec un champ électrique dirigé de la gauche vers la droite. Derrière le deuxième cylindre, on a un troisième cylindre relié à l’inverse des autres cylindres : le côté positif à droite et négatif à gauche. Le champ électrique est donc dirigé vers la gauche, à l’inverse des autres cylindres. Le quatrième cylindre est chargée de la même façon que les deux autres cylindres précédents.
Si on lâche une particule dans l’espace entre les deux premiers cylindres, elle va se faire accélérer. Elle va ensuite rentrer dans le deuxième cylindre à une vitesse constante. A la fin de ce cylindre, le champ électrique sera face à elle. En fait, cette tension est une tension alternative, tantôt positive, tantôt négative. On s’arrange donc pour que le changement ait lieu juste au moment où la particule est dans le deuxième interstice. La tension est inversée et les charges aux bornes du générateur aussi. Cela va inverser le champ électrique et il sera de nouveau dirigé vers la droite. La particule sera de nouveau accélérée. Et ainsi de suite.
Les tubes doivent être de plus en plus long car les particules prennent de plus en plus de vitesse ! Cela permet de prendre en compte le fait que la particule va prendre plus de distance dans une même durée.


