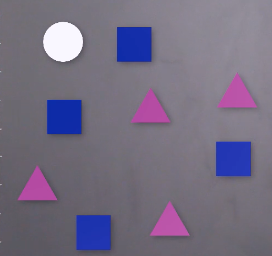Évolution génétique des populations et impact des activités humaines
Évolution génétique des populations
Évolution génétique des populations
I. L’histoire du modèle de Hardy-Weinberg et ses hypothèses
Godfrey Hardy est un mathématicien anglais ayant exercé à Cambridge au début du XXe siècle. Un de ses amis, Reginald Punnett, fut pris dans une controverse autour de la génétique et de la biologie évolutive. Des opposants de Punnett avançaient que la proportion d’individus portant certains allèles ne cesserait d’augmenter dans la population.
Hardy s’engagea donc par amitié à prouver que, quelle que soit la répartition des génotypes dans la population de départ, cette répartition devient stable dès la 2e génération. Pour cela, il se fonda sur les hypothèses suivantes :
|
Hypothèses portant sur la population de départ |
Hypothèses portant sur les mécanismes évolutifs |
|
– Population de taille infinie – Pangamie (= croisement aléatoire d’individus où tous les gamètes ont la même chance d’être produits) – Panmixie (=formation aléatoire des couples et donc rencontre aléatoire des gamètes) |
Absence de mutation sur les allèles étudiés |
|
Espèce considérée diploïde (2n chromosomes) et à reproduction sexuée |
Absence de migration (la population étudiée est isolée) |
|
Générations non chevauchantes |
Absence de sélection |
II. Description de la structure génétique d’une population
|
Tableau de croisement (cas d’un gène avec deux allèles A et a) |
Gamète femelle |
||
|
A (p) |
a (q) |
||
|
Gamète mâle |
A (p) |
AA (p²) |
Aa (pq) |
|
a (q) |
Aa (pq) |
aa (q²) |
|
$p + q = 1$
$p^2 + 2pq + q^2 = 1$
Pour décrire la structure génétique d’une population, il convient de distinguer :
– Les fréquences génotypiques : c’est-à-dire les fréquences de chaque génotype au sein de la population (exemple : fréquence du génotype AA dans la descendance, ici ¼).
– Les fréquences alléliques : c’est-à-dire les fréquences de chaque allèle au sein de la population.
Exemple : fréquence de l’allèle A dans la descendance :
$FA = f(A//A) + dfrac{1}{2} f(A//a)$
$FA = p^2 + dfrac{1}{2} (2pq) = p^2 = pq = p (p+q)$
D’ou $FA = p$
Au cours de l’évolution biologique, la composition génétique des populations d’une espèce change de génération en génération. Le modèle mathématique de Hardy-Weinberg utilise la théorie des probabilités pour décrire le phénomène aléatoire de transmission des allèles dans une population.
En assimilant les probabilités à des fréquences pour des effectifs de grande taille (loi des grands nombres), le modèle prédit que la structure génétique d’une population de grand effectif est stable d’une génération à l’autre sous certaines conditions (absence de migration, de mutation, de sélection). Cette stabilité théorique est connue sous le nom d’équilibre de Hardy-Weinberg.
III. Les écarts à l’équilibre de Hardy-Weinberg
Les conditions de l’équilibre de Hardy-Weinberg ne sont pas courantes dans la nature. En effet, les écarts entre les fréquences observées sur une population naturelle et les résultats du modèle s’expliquent notamment par les effets de forces évolutives (mutation, sélection naturelle, dérive génétique, reproduction asexuée, etc.)
Impact de activités humaines sur la biodiversité
Impact de activités humaines sur la biodiversité
I. Les activités humaines entrainent l’extinction des espèces
Les activités humaines (pollution, destruction des écosystèmes, combustions et leurs impacts climatiques, surexploitation d’espèces…) ont des conséquences sur la biodiversité et ses composantes (dont la variation d’abondance) et conduisent à l’extinction d’espèces.
La biodiversité peut être estimée de différentes manières. La richesse spécifique correspond au nombre d’espèces présentes dans un milieu alors que l’abondance représente le nombre d’individus de la même espèce. Dans un milieu contenant plusieurs espèces l’équitabilité estime si l’abondance entre chaque espèce est équilibrée.
|
|
Richesse spécifique : 4 triangles ; 4 carrés ; 4 ronds = 3 espèces espèces différentes Abondance des espèces (4 individus par espèce) Equitabilité (abondance comparable) |
|
|
Si une espèce (rond) est surexploitée par l’humain : Disparition de 3 ronds |
|
|
Le réchauffement climatique, la destruction des habitats, les activités humaines peuvent une espèce : Disparition de 4 triangles |
|
Finalement, la richesse spécifique a diminué (plus que 2 espèces), l’abondance a diminué (1 seul rond). Ainsi, les activités humaines diminuent la biodiversité et peut même mener à une extinction d’espèce (triangle) |
|
II. La fragmentation de l’habitat des espèces par la présence des activités humaines
En plus de fragmenter les habitats naturels en plusieurs zones isolées, la présence de routes réduit la surface disponible pour les espèces et apporte également un danger à cause du passage des voitures. Actuellement 70 % de la forêt mondiale se trouve à moins de 1 km de la lisière à cause de la fragmentation. De nombreuses espèces d’animaux et de végétaux ne peuvent vivre à proximité de la lisière car les conditions de vie y sont différentes (insolations, vents, écarts thermiques) : c’est l’effet lisière.
On peut estimer l’impact de la fragmentation en utilisant un quadrillage et en calculant la surface occupée par les infrastructures humaines :
– Au départ, nous avons 8 carrés de 50 m, c’est-à-dire une surface totale de 400m * 400m = 160 000 m² = 160 km²
– Si on construit une route au milieu de cette surface : 400m * 150m = 60 000 m² * 2 = 120 km²
– Perte de 40 km² habitables
Sachant que la densité de population ne peut pas excéder un certain nombre d’individus/km², on comprend alors que la fragmentation d’une population en plusieurs échantillons de plus faibles effectifs entraîne par dérive génétique un appauvrissement de la diversité génétique d’une population.
III. La préservation de la biodiversité
La connaissance et la gestion d’un écosystème permettent d’y préserver la biodiversité.

Crapeauduc : tunnel pour batraciens et autres petits animaux. Un système destiné à protéger les amphibiens pendant leurs phases migratoires.
Les chauves-souris peuvent emprunter les passages aériens qu’on leur a construits, ce qui permet de rétablir en partie la connexion entre les populations séparées par la route. Ces passages doivent être précisément localisés, et il faut pour cela étudier en détail les endroits où les individus franchissent la route. Il suffit parfois de quelques mètres de différence pour que les individus n’empruntent pas le passage qu’on leur a construit.