Dérive génétique et sélection naturelle
La dérive génétique et la sélection naturelle sont deux phénomènes évolutifs majeurs. Pour illustrer la dérive génétique, voici l’exemple d’une population contenant des souris noires et d’autres blanches. Seulement 20 individus composent cette population : 10 souris blanches, 10 souris noires. On peut remarquer que l’effectif de cette population est très faible.
Après 100 générations, et en laissant intervenir uniquement le hasard, un des deux allèles responsables de la couleur noire ou blanche va être fixé : les souris deviennent homozygotes.
Après 100 générations, le hasard aura fait que 100 % des souris seront noires, par exemple. Ou blanches. Ou encore 70 % noires, 30 % blanches, car voir diminuer la fréquence d’une couleur de souris est le reflet de la fixation progressive de l’allèle responsable de cette couleur.
La fixation d’un caractère dans une population possédant un effectif réduit est appelée effet fondation. Il est le témoin d’une perte de diversité génétique. Cette perte de diversité peut avoir de lourdes conséquences, car une espèce dont la diversité est réduite aura plus de mal à s’adapter à certains environnements.
Par exemple, si l’on imagine nos 20 souris noires et blanches au sein d’un environnement très enneigé, il est logique de considérer que les souris blanches arriveront mieux à se cacher, et seront donc moins visibles par les prédateurs que les noires. Elles auront un meilleur succès reproductif (ou fitness) et engendreront plus de descendance. La fréquence de l’allèle responsable de la couleur blanche l’emportera donc rapidement sur celle de l’allèle responsable de la couleur noire. Dans ce cas précis, où la population subit une pression due à l’environnement, on ne parle plus uniquement de dérive génétique mais également de sélection naturelle. Ce n’est plus seulement le hasard qui influence la fréquence des allèles, la pression environnementale joue aussi un rôle.
L‘évolution de la biodiversité dépend donc de la dérive génétique (du hasard) ainsi que de la sélection naturelle (de l’impact de l’environnement sur l’effectif des populations, sur leur phénotype).
Le modèle de Hardy-Weinberg
Ce modèle est utilisé lorsqu’on cherche à connaître la structure génétique d’une population. Dans un premier temps on définit ce qu’est une population.
Une population est un groupement d’individus spatialisés, donc délimités dans un espace réduit, et appartenant à la même espèce.
I. Ernst Mayr : la population comme unité d’évolution
Ernst Mayr, biologiste allemand, considère la population comme l’unité d’évolution. Quand on veut regarder à grande échelle de temps comment évoluent les individus, on étudie un ensemble d’individus, autrement dit une population. Ernst Mayr propose que le gène soit l’unité héréditaire : ce que l’on transmet aux générations. Si on veut être plus précis, on parle d’allèles. L’individu est l’unité sélectionnée puisqu’un individu est un phénotype (un ensemble de caractère observables). Dans un environnement donné, ce phénotype sera plus ou moins adapté, apportera un avantage adaptatif ou non à l’individu donc ce sera l’unité de sélection.
II. Le modèle statistique de Hardy-Weinberg
L’idée de ce modèle est de trouver des fréquences génotypiques attendues en fonction des fréquences alléliques. On a une population, des fréquences alléliques et on en déduit des fréquences génotypiques théoriques. On compare la théorie aux valeurs mesurées et on peut savoir si la population est dite à l’équilibre ou non.
Quelles sont les conditions pour être à l’équilibre structurel d’un point de vue génétique pour une population ?
La construction de ce modèle repose sur différentes hypothèses. On part nécessairement d’individus diploïdes et d’une population dite infinie. Dans la pratique, on considère que 1 000 individus est infini. Il faudra que ces individus ne se choisissent pas d’un point de vue reproduction sexuée, autrement dit qu’il y ait une panmixie (rencontre complètement aléatoire des individus), voire même une pangamie (les gamètes ne se choisissent pas, les rencontres gamétiques sont aléatoires).
Pour que cette structure génétique fonctionne, il ne faut pas de force évolutive (pas de dérive génétique, pas de sélection naturelle, pas de migration, ni de mutation).
Si toutes ces conditions sont réunies, l’équilibre Hardy-Weinberg dit que si l’on considère un gène qui a deux allèles ($A$ et $a$), que la fréquence de l’allèle $A$ vaut $p$ : $f(A) =p$ et que la fréquence de l’allèle a vaut $q$ : $f(a) =q,$ on peut en déduire la fréquence des génotypes.
Le génotype $AA$ aura pour fréquence $p^2 : f(AA) = p^2.$
Le génotype $Aa$ aura pour fréquence $2pq : f(Aa) = 2pq.$
Le génotype $aa$ aura pour fréquence $q^2: f(aa) = q^2,$ avec $p^2 + q^2 + 2pq = 1,$ et $p + q = 1.$
III. Explication du modèle
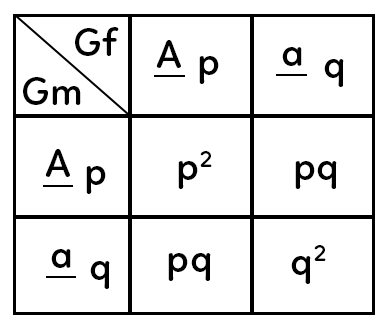
Voici un échiquier de croisements des gamètes.
Puisqu’on part du postulat que les individus sont hétérozygotes pour le gène considéré, le gamète femelle est de génotype $Aa$ (possède l’allèle $a$ et l’allèle $A$).
On pose $f(A) = p$ et on reporte cette fréquence dans l’échiquier des gamètes, de même que $f(a) = q.$
Il en est de même pour le gamète mâle : l’individu mâle produit avec une fréquence $p$ des individus $A$ et avec un fréquence $q$ des individus $a.$
À la descendance, qu’obtient-on une fois ces gamètes croisés ?
$p times p = p^2,$
$p times q$ deux fois $= 2pq,$
$q times q = q^2.$
On comprend que si l’on considère la totalité de la descendance obtenue (fréquence totale des génotypes : 1), on aura $p^2+ q^2+ 2pq.$
On peut le traduire graphiquement avec la fréquence des génotypes en ordonnée. On utilise Hardy-Weinberg pour trouver la fréquence des génotypes grâce à la fréquence des allèles.
Combien de génotypes possibles a-t-on quand on étudie un gène bi-allélique ?
On a trois génotypes possibles : $AA, Aa$ et $aa.$
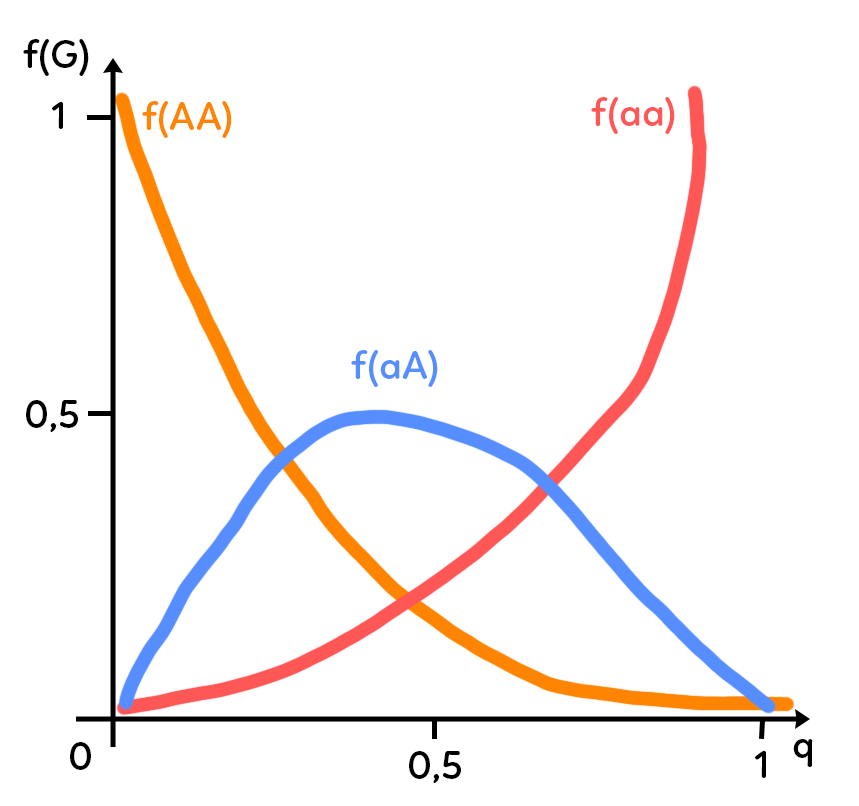
Si on exprime la fréquence du génotype $AA$ en fonction de $q,$ la fréquence de $a,$ on constate que lorsqu’on a une fréquence de $a$ très faible, la fréquence de $AA$ est très forte, puisque $f(AA)= p^2,$ or plus $q$ est petit, plus $p$ est grand puisque $p + q =1.$
En ce qui concerne $f(aa)$ c’est la symétrie parfaite de $f(AA),$ puisque $f(aa) = q^2.$
Enfin pour $f(Aa),$ qui vaut $2pq,$ la courbe a une forme de polynôme du second degré avec nécessairement un maximum atteint à 0,5 : on ne peut pas avoir plus de 50 % d’hétérozygotes $Aa$ car $2pq,$ la fréquence de ce génotype, vaut au maximum 0,5 (valeur maximale pour $p = 0,5$ ; valeur maximale pour $q = 0,5$ ; du fait que $p + q = 1$ ; et $2 times 0,5 times 0,5 = 0,5$).
Conclusion
Le modèle de Hardy-Weinberg est une théorie. Lorsque les résultats observés s’éloignent de la théorie cela signifie qu’une des hypothèses sur lesquelles il repose, voire plusieurs, ne sont pas confirmées. Peut-être que la population n’est pas infinie, peut-être qu’il n’y a pas panmixie ou pangamie, peut-être qu’il y a une force évolutive qui s’exerce sur la population qu’on observe.



.png?1532593935845)