Fonctions homographiques - Le rappel de cours
Fonctions homographiques
Définition
Pour tout $x \in \mathbb{R} \backslash \left\{\dfrac{-d}{c}\right\}$, on peut définir une fonction homographique comme étant la fonction
$ f(x) = \dfrac{ax+b}{cx+d} $, où $a,b,c$ et $d$ sont des réels. ($c$ et $d$ non tous nuls)
Autre notation
Pour tout $x \in \mathbb{R} \backslash \{\alpha\}$, on peut définir une fonction homographique comme étant la fonction
$ f(x) = \dfrac{a}{x – \alpha} + \beta$, où $a, \alpha, \beta$ sont des réels.
Variations
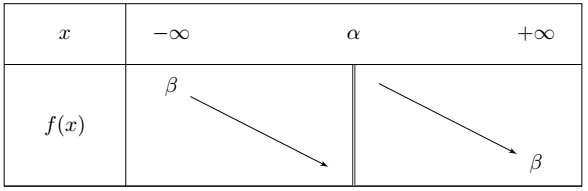
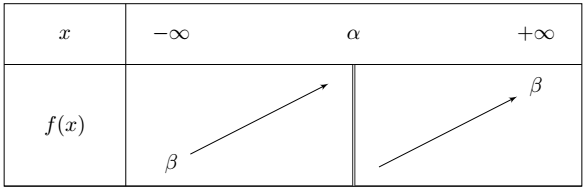
Les variations sont déterminées à partir du signe de $a$.
Si $a>0$, le tableau de variations est le suivant :
Si $a<0$, le tableau de variations est le suivant :
Les doubles barres signifient que la valeur $x = \alpha$ est un valeur interdite car la fonction n’est pas définie pour cette valeur.
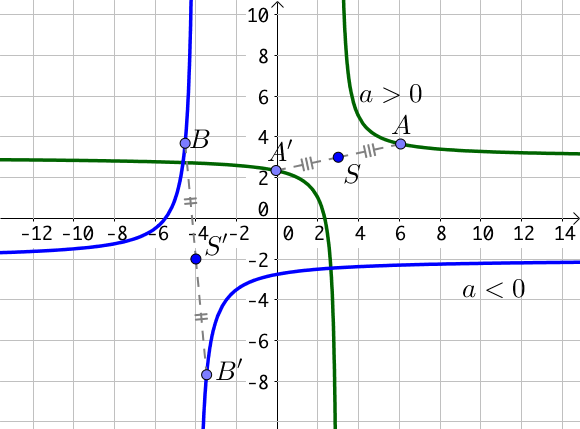
Le point $S(\alpha; \beta)$ est le centre de symétrie de l’hyperbole qui est différent de l’origine du repère si $\alpha \neq 0, \beta \neq 0$.