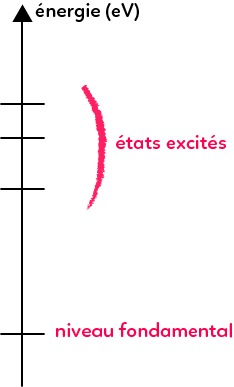Lumière : onde ou particule ?
Lumière : onde ou particule ?
On sait déjà que la lumière peut être considérée comme une particule, avec notamment, l’effet photoélectrique. C’est une particule particulière de lumière appelée photon. Et on a vu aussi que la lumière peut être considérée comme une onde avec les phénomènes d’interférences et de diffraction.
Quelles sont les formules à retenir pour l’aspect particulaire de la lumière ?
Il y a la formule de l’énergie d’un photon : $E = h\times ν = \dfrac{h\times c}{\lambda}$
L’énergie est en joules (J), c est la constante de la vitesse de la lumière dans le vide (3,00.108 m.s-1), $h$ la constante de Planck est donnée dans les exercices avec plus ou moins de chiffres significatifs (6,63.10-34 J.s, on a trois chiffres significatifs pour être cohérents avec le nombre de chiffres significatifs de $c$), $\lambda$ a longueur d’onde en mètres (m).
Pour rappel, la longueur d’onde caractérise la couleur de l’onde, donc la couleur du photon. Ce qu’il faut comprendre dans cette formule, c’est le rapport entre la longueur d’onde et l’énergie. Quand la longueur d’onde est petite, l’énergie est grande, dû à l’inverse de la proportionnalité. Inversement, si la longueur d’onde est grande, l’énergie va être petite. Dans les exercices, il faut trouver l’énergie grâce à la longueur d’onde.
La relation qui s’ajoute à cela est la relation de Louis de Broglie :
$p = m\times v$ et $p = \dfrac{h}{\lambda}$
Les relations font intervenir : $p$, l’impulsion, $h$ la constante de Planck et $\lambda$ la longueur d’onde. Ces sont des relations qu’il faut connaître. Elles font le lien entre la lumière qui correspond à une particule et la lumière qui correspond à une onde. Les phénomènes ondulatoires vus sur les chapitres sur l’interférence et la diffraction ne sont observables que sur des petites longueurs d’ondes. Donc, ici, si la longueur d’onde est petite, l’impulsion correspondante sera grande.
Ce qui est intéressant avec cette formule c’est qu’elle est valable pour toutes les particules (pas seulement pour la lumière) comme les électrons, par exemple. Si la longueur d’onde est grande, l’impulsion va être petite. Et, si la longueur d’onde est grande, on observera plus de phénomène ondulatoire mais on n’observera seulement des effets particulaires.
Interaction lumière - matière
Voyons comment lumière et matière interagissent, ce qui va nous permettre d’expliquer les spectres de raies d’émission et les spectres de raies d’absorption.
Lumière => photon
La lumière peut être considérée comme un transport de corpuscules, ces corpuscules sont les photons. On considère un rayonnement électromagnétique monochromatique caractérisé par une longueur d’onde $λ$ exprimée en mètres et par sa fréquence $ν$ exprimée en Hertz. Chaque photon qui constitue ce rayonnement monochromatique transporte une quantité d’énergie appelée quantum d’énergie, que l’on peut calculer de la manière suivante :
$ΔE = hν$, avec $h$ la constante de Planck, $ν$ étant la fréquence du rayonnement exprimée en Hz.
On a la relation : $ν = \dfrac{c}{ λ }$, avec $ν$ la fréquence en Hz, $c$ la célérité de la lumière dans le vide en m.s-1 et $λ$ en m. On peut retrouver cela facilement en analysant les unités. On a des m.s-1 divisés par des m donc on a des s-1 ce qui est bien homogène à une fréquence.
On peut dire également que : $ΔE = hν = \dfrac{hc}{ λ }$.
On parle de quantification de l’énergie puisque le photon ne peut pas transporter n’importe quelle valeur de l’énergie mais une valeur déterminée de l’énergie. C’est la même chose au niveau de la matière.
Matière => niveau d’énergie
L’énergie est quantifiée, elle ne peut pas prendre toutes les valeurs mais peut prendre certaines valeurs qui sont représentées sur un diagramme d’énergie où l’énergie est couramment exprimée en électrons-Volts (eV) et non pas en Joules. On donnera la conversion eV/J et il suffira de faire la conversion à ce moment-là. Le niveau d’énergie le plus bas que peut avoir l’atome c’est l’état fondamental. Les niveaux d’énergie supérieurs à l’état fondamental sont appelés les états excités. On utilise ces diagrammes d’énergie pour expliquer les interactions entre la lumière et la matière.
Interactions lumière-matière
La lumière et la matière interagissent à travers les phénomènes d’émission et d’absorption de lumière.
Émission de lumière
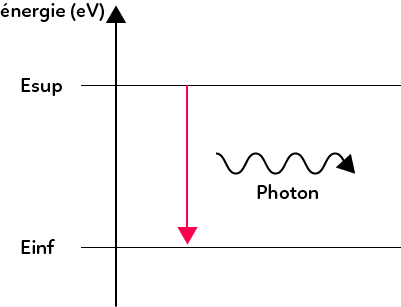
On a émission de lumière lorsqu’un atome est à un état d’énergie supérieur (état excité) et qu’il perd cette énergie pour passer dans un état d’énergie inférieur (qui peut être un autre état excité d’énergie plus basse ou alors à nouveau l’état fondamental). On représente cette perte d’énergie par une flèche vers le bas.
Lorsque l’atome perd cette énergie, il émet un photon de longueur d’onde bien déterminée. Pour déterminer cette longueur d’onde, il suffit d’utiliser la formule : $ΔE = \dfrac{hc}{ λ }$ donc la longueur d’onde du photon émis est égale à $ λ = \dfrac{hc}{ΔE}$. Ici la variation d’énergie vaut $E_{sup}-E_{inf}$ donc : $λ = \dfrac{hc}{E_{sup}-E_{inf}}$.
Remarque : sur certains diagrammes d’énergie on donne les énergies avec des chiffres négatifs et sur d’autres on trouve des énergies avec des signes positifs. Ce qui compte c’est la différence d’énergie alors que ce soit compté positivement ou négativement revient au même.
Absorption de lumière
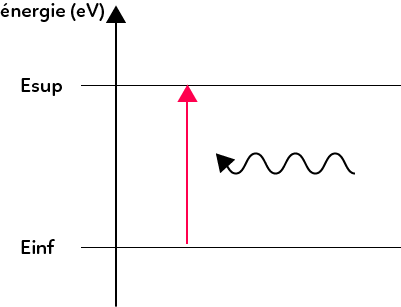
Lorsqu’un atome absorbe de la lumière, il gagne de l’énergie. Il passe d’un état d’énergie inférieur à un état d’énergie supérieur.
On passe par ces deux étapes en absorbant un photon. Pour connaître la longueur d’onde du photon qui est absorbé, on utilise exactement la même formule : $λ = \dfrac{hc}{E_{sup}-E_{inf}}$.
C’est la même formule, mais les deux phénomènes sont différents et il faut être capable de calculer la longueur d’onde du photon émis ou absorbé et être capable de reconnaître si l’on est dans le cas de l’émission (flèche vers le bas, photon émis, perte d’énergie de l’atome) ou dans le cas de l’absorption (flèche vers le haut, photon absorbé, gain d’énergie de l’atome).
Niveau d'intensité sonore
Les ondes sonores sont des ondes mécaniques, qui se définissent par la propagation d’une perturbation locale dans un milieu matériel sans déplacement global de matière.
I. La naissance de l’onde sonore
La membrane d’un haut parleur, bien que restant verticale, possède un mouvement horizontal à l’origine d’une perturbation, comprimant l’air lorsqu’elle avance et le dilatant lorsqu’elle recule, modifiant ainsi sa pression et donnant naissance à un son.
Lors des différentes phases de compression/dilatation, la perturbation se propage de proche en proche.
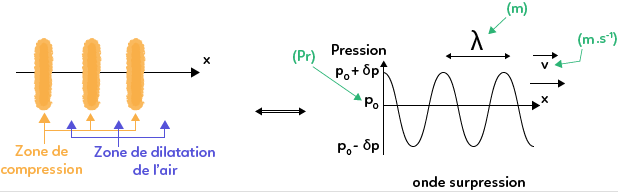
Ainsi observe-t-on dans l’espace une succession de zones de compression et de zones de dilatation de l’air.
Si on s’intéresse à l’évolution de la pression en fonction de la position, on remarque des zones de surpression, c’est-à-dire des parties où la pression est supérieure à la pression moyenne, qui correspondent aux zones de compression de l’air et des zones où la pression est inférieure à la pression moyenne qui sont les zones de dilatation de l’air.
De plus, un son pur est modélisé par une sinusoïde, qui est une fonction périodique, et est donc caractérisé par une longueur d’onde $\lambda$ et une célérité $c$.
II. L’intensité acoustique
L’onde se propageant depuis la source peut rencontrer lors de son parcours un récepteur.
En outre, bien qu’il n’y ait pas de transport de matière, la propagation de l’onde s’accompagne d’un transport d’une puissance sonore $P$ (en Watt), reçue sur une surface $S$ (en $\text{m}^2$) par le récepteur.
L’intensité acoustique $I$ (en $\text{W.m}^{-2}$) est ainsi définie par : $I = \dfrac{P}{S}$.
III. Le niveau sonore
L’intensité acoustique prend cependant des valeurs très éparses, s’étalant de $10^{-12}\text{ W.m}^{-2}$ pour le seuil de l’audibilité à $1\text{W.m}^{-2}$ pour le seuil de la douleur.
Pour réduire cette disparité des valeurs, on calcule le niveau sonore qui utilise la fonction logarithme ($\log$) et dont la formule est :
$L = 10 \times \log \left(\dfrac{I}{I_0} \right)$, où $L$ est le niveau sonore (en dB), $I$ est l’intensité sonore et $I_0 = 10^{-12} \text{ W.m}^{-2}$, qui correspond au seuil d’audibilité.
IV. Cas avec plusieurs sources
Ce sont les intensités sonores que l’on ajoute et non pas les niveaux sonores.
On considère deux haut-parleurs émettant tous deux un son en direction du récepteur de niveau sonore $60 \text{dB}$. Afin de connaître le niveau sonore au niveau du récepteur, on ne peut pas ajouter le niveau sonore de chacune des deux sources, on doit donc trouver leur intensité sonore.
On utilise donc pour ce faire la formule suivante : $I = I_0 \times 10^L $.
Ainsi, on a :
$ I_{tot} = I_1 + I_2 $
$ I_{tot} = I_0 \times 10^{L_1} \ + \ I_0 \times 10^{L_2} $
$ I_{tot} = 2 . 10^{-6} \text{W/m}^2 $
soit encore $L_{tot} = 10 \times \log{\left(\dfrac{I_{tot}}{I_0} \right)} = 63 \text{ dB}$
En conclusion, multiplier par deux l’intensité sonore revient à ajouter $3 \text{ dB}$ au niveau sonore.