Échelle d'une carte
Echelle d’une carte
Définition
L’échelle d’une carte est définie comme étant le rapport de la dimension de la carte par la dimension réelle, c’est à dire
$\text{échelle} = \dfrac{\text{dimension de la carte}}{\text{dimension réelle}}$.
Utiliser une échelle
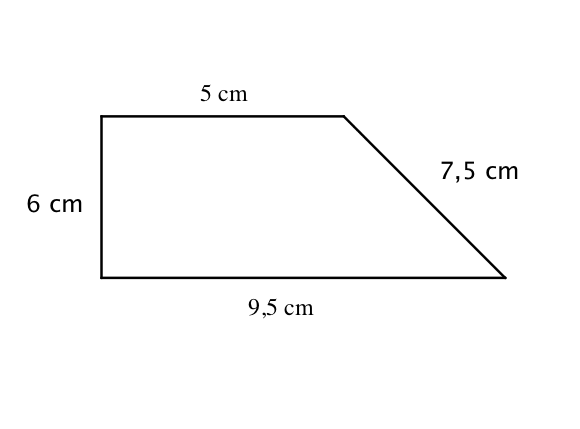
On donne une figure représentant un terrain à l’échelle $1/1000$ et on cherche les dimensions réelles.
L’échelle $1/1000$ signifie que 1 cm sur la carte représente 1 000 cm dans la réalité. On prendra garde au fait que les longueurs doivent avoir la même unité.
Pour trouver les dimensions, on sait que les mesures de la carte sont proportionnelles aux longueurs réelles : on peut donc utiliser un tableau de proportionnalité, en plaçant sur la première ligne les dimensions sur le plan (en cm) et sur la seconde les dimensions réelles (en cm), dont le coefficient de proportionnalité est égal à l’inverse de l’échelle.
| Dimensions sur le plan (en cm) | 5 | 7,5 | 9,5 | 6 |
| Dimensions réelles (en cm) | ? | ? | ? | ? |
On utilise le coefficient de proportionnalité pour trouver les valeurs réelles, en multipliant ainsi par $1000$ les dimensions sur le plan.
Ainsi, le tableau après calcul est le suivant.
| Dimensions sur le plan (en cm) | 5 | 7,5 | 9,5 | 6 |
| Dimensions réelles (en cm) | 5000 | 7500 | 9500 | 6000 |
Calculer une échelle
La méthode pour calculer une échelle est expliquée à travers un exemple.
Sur une carte routière, la distances entre deux villes est de 15 cm. En réalité, elles sont séparées de 300 km.
Quelle est l’échelle de cette carte ?
Comme les dimensions de la carte sont proportionnelles aux dimensions réelles on utilise un tableau de proportionnalité dont le coefficient est l’inverse de l’échelle.
Or les longueurs doivent être exprimées dans la même unité. Ainsi on exprime les longueurs en centimètres, et alors 300 km = 30 000 000 cm.
| Distances sur la carte (en cm) | 15 |
| Distances réelles (en cm) | 30 000 000 |
On cherche le coefficient de proportionnalité qui permet de passer de la première ligne à la seconde. Il vaut donc $ \dfrac{15}{30000000} = 0,000 000 5$.
Enfin, comme l’échelle est égale à l’inverse de ce coefficient, on trouve
$\dfrac{1}{0,000 000 5} = 2 000 000$.
L’échelle est donc $1/2 000 000$.