Angles

Natures des angles

Angles, rapporteurs, bissectrices

À retenir : Pour construire un angle on trace deux demi-droites (les côtés de l’angle)  de même origine (le sommet de l’angle).

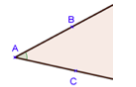
Le point A est le sommet de l’angle $\widehat{BAC}$. 

Les demi-droites [AB) et [AC) sont les côtés de l’angle$\widehat{BAC}$.

Pour tracer ou mesurer un angle on utilise un rapporteur gradué en degrés (noté °). Il faut être très précis en plaçant le centre (ou la croix) du rapporteur sur le sommet de l’angle ; et le 0° de la graduation sur un des côtés de cet angle.

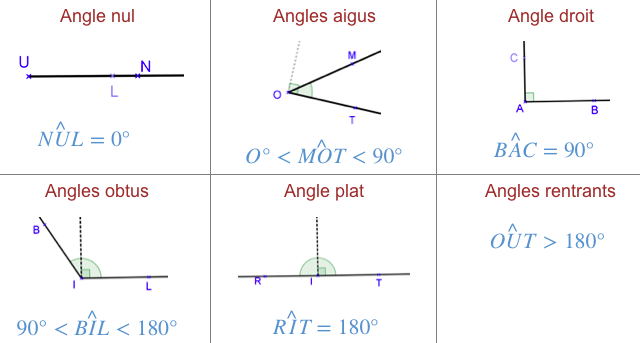
Natures et mesures des angles à connaître :

Les angles nul, aigu, droit, obtus et plat (donc entre 0° et 180°) sont des angles saillants.

Propriétés

Si trois points R, I et T sont alignés dans cet ordre alors $\widehat{RIT}=180°$.

Si  $\widehat{RIT}=180°$ (c’est-à-dire si $\widehat{RIT}$ est un angle plat) alors les points R, I et T  sont alignés dans cet ordre.

Bissectrice, Définition :

La bissectrice d’un angle est la demi-droite qui partage l’angle en deux angles adjacents et de même mesure.

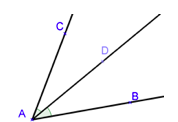
Exemple :

[AD) est la bissectrice de l’angle  donc par exemple si $\widehat{CAB}$ mesure 64°, alors $\widehat{CAD}$et $\widehat{DAB}$ mesurent chacun 32°    $(64 \div 2=32)$

Commentaire : Il faut toujours penser, que l’on peut prolonger les côtés d’un angle (ce sont des demi-droites !) en particulier pour mesurer l’angle avec le rapporteur.

Tracer une bissectrice

A retenir :
La bissectrice d’un angle est une demi-droite qui partage cet angle en deux angles adjacents et de même mesure.