Niveau d’intensité sonore
I. Définition d’une onde sonore
Comment définir une onde sonore ?
Les ondes sonores sont des ondes mécaniques, qui se définissent par la propagation d’une perturbation locale dans un milieu matériel sans déplacement global de matière.
II. La naissance de l’onde sonore
Comment se produit une onde sonore ?
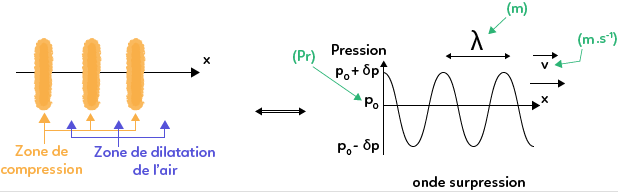
La membrane d’un haut parleur, bien que restant verticale, possède un mouvement horizontal à l’origine d’une perturbation, comprimant l’air lorsqu’elle avance et le dilatant lorsqu’elle recule, modifiant ainsi sa pression et donnant naissance à un son.
Lors des différentes phases de compression/dilatation, la perturbation se propage de proche en proche.
Ainsi observe-t-on dans l’espace une succession de zones de compression et de zones de dilatation de l’air.
Si on s’intéresse à l’évolution de la pression en fonction de la position, on remarque des zones de surpression, c’est-à-dire des parties où la pression est supérieure à la pression moyenne, qui correspondent aux zones de compression de l’air et des zones où la pression est inférieure à la pression moyenne qui sont les zones de dilatation de l’air.
De plus, un son pur est modélisé par une sinusoïde, qui est une fonction périodique, et est donc caractérisé par une longueur d’onde $\lambda$ et une célérité $c$.
III. L’intensité acoustique
Comment déterminer l’intensité acoustique ?
L’onde se propageant depuis la source peut rencontrer lors de son parcours un récepteur.
En outre, bien qu’il n’y ait pas de transport de matière, la propagation de l’onde s’accompagne d’un transport d’une puissance sonore $P$ (en Watt), reçue sur une surface $S$ (en $\text{m}^2$) par le récepteur.
L’intensité acoustique $I$ (en $\text{W.m}^{-2}$) est ainsi définie par : $I = \dfrac{P}{S}$.
IV. Le niveau sonore
Comment déterminer le niveau sonore ?
L’intensité acoustique prend cependant des valeurs très éparses, s’étalant de $10^{-12}\text{ W.m}^{-2}$ pour le seuil de l’audibilité à $1\text{W.m}^{-2}$ pour le seuil de la douleur.
Pour réduire cette disparité des valeurs, on calcule le niveau sonore qui utilise la fonction logarithme ($\log$) et dont la formule est :
$L = 10 \times \log \left(\dfrac{I}{I_0} \right)$, où $L$ est le niveau sonore (en dB), $I$ est l’intensité sonore et $I_0 = 10^{-12} \text{ W.m}^{-2}$, qui correspond au seuil d’audibilité.
V. Cas avec plusieurs sources
Ce sont les intensités sonores que l’on ajoute et non pas les niveaux sonores.
On considère deux haut-parleurs émettant tous deux un son en direction du récepteur de niveau sonore $60 \text{dB}$. Afin de connaître le niveau sonore au niveau du récepteur, on ne peut pas ajouter le niveau sonore de chacune des deux sources, on doit donc trouver leur intensité sonore.
On utilise donc pour ce faire la formule suivante : $I = I_0 \times 10^L $.
Ainsi, on a :
$ I_{tot} = I_1 + I_2 $
$ I_{tot} = I_0 \times 10^{L_1} \ + \ I_0 \times 10^{L_2} $
$ I_{tot} = 2 . 10^{-6} \text{W/m}^2 $
soit encore $L_{tot} = 10 \times \log{\left(\dfrac{I_{tot}}{I_0} \right)} = 63 \text{ dB}$
En conclusion, multiplier par deux l’intensité sonore revient à ajouter $3 \text{ dB}$ au niveau sonore.
Atténuation du signal
I. Définition de l’atténuation d’un signal
Qu’est-ce que l’atténuation d’un signal ?
On parle de l’atténuation d’un signal et donc on définit l’atténuation en décibel et l’atténuation linéique. C’est principalement dû au canal de transmission dans la chaîne d’informations. Le canal de transmission présente une certaine puissance notée Pe en entrée et Ps en sortie. Le canal idéal est $Ps = Pe$ : c’est-à-dire que ressort ce qui est rentré. Mais ce canal n’existe pas. Il y a forcément une atténuation car le signal peut-être légèrement perdu, absorbé, etc., en fonction des situations.
II. Atténuation en décibel (dB)
Pourquoi ne calcule-t-on pas l’atténuation comme la puissance de sortie divisée par celle d’entrée ?
Comme parfois la division $\dfrac{Ps}{Pe}$ est extrêmement grande, on préfère introduire le décibel avec la fonction log. Voici la formule : $A_{dB} = 10log \dfrac{Pe}{Ps}$.
La puissance en entrée et en sortie est exprimée en Watts (W), l’atténuation est en décibel (dB). Le rapport est sans unité car on divise des Watts par des Watts donc l’atténuation est une quantité sans unité. On précise « dB » car on a utilisé le « 10log ».
Exemple
Soit une transmission avec une atténuation de 4dB. Si Pe = 10W, que vaut Ps ?
On ne peut pas utiliser la formule telle quelle car elle permet de calculer l’atténuation quand on connaît la puissance en entrée et celle en sortie. Le but étant d’obtenir Ps, on va devoir l’isoler. Dans un premier temps, on fait passer le 10 à gauche :
$ \dfrac{A_{dB}}{10} = log \dfrac{Pe}{Ps}$.
Il faut se débarrasser du log, pour cela on utilise la fonction réciproque qui est la fonction 10 puissance.
On applique cette fonction : $\dfrac{Pe}{Ps} = 10^{\frac{A_{dB}}{10}}$.
Ensuite on isole Ps : $Ps = \dfrac{Pe}{10^{\frac{A_{dB}}{10}}} = Pe \times 10^{\frac{-A_{dB}}{10}} $.
Si on se fie au chiffre présenté plus haut, cela nous donne $4,0W$ environ.
III. Atténuation linéique
Dans certains exercices, on donne par exemple une fibre optique et on dit que son atténuation est de 3dB/km. C’est une atténuation linéique. Voici la formule : $α = \dfrac{A_{dB}}{L}$.
L’atténuation linéique est en dB.m-1 ou dB.km-1, l’atténuation totale est en dB et la longueur du canal de transmission L est en $m$ ou en $km.$ Cela peut être une fibre optique, l’air, un câble coaxial, une prise électrique, etc.
Par exemple, si une fibre de 200 km a une atténuation totale de 80dB, son atténuation linéique vaut : $ α = \dfrac{80}{200} = 0,4 dB/km$.
On peut avoir des exercices où on demande aussi de calculer l’atténuation totale sachant qu’on donne l’atténuation linéique et la longueur. Ce qui permet éventuellement de réutiliser la formule précédente.