Équation cartésienne de cercle
Équation cartésienne de cercle
Pour trouver l’équation d’un cercle, il existe deux manières de procéder selon que l’on dispose du centre et du rayon ou du diamètre.
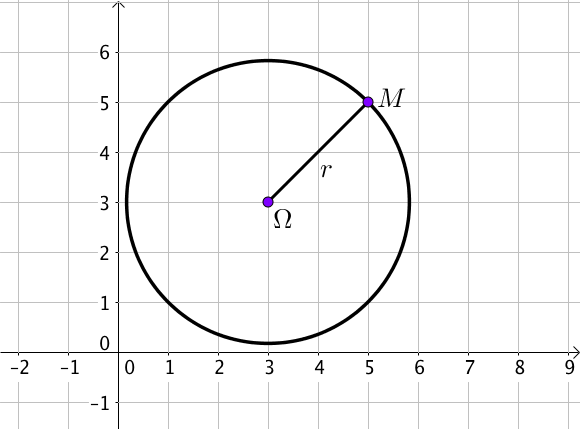
1) Avec le centre $\Omega (a; b)$ et le rayon $r$
Soit $M(x; y)$ un point du cercle,
Alors ${\Omega M}^2 = r^2$.
Ainsi, $(x – a)^2 + (y – b)^2 = r^2$.
Exemple :
Si $\Omega (-1; 2)$ et $r = 3$, alors l’équation réduite du cercle est
$(x – (-1))^2 + (y – 2)^2 = 3^2$ c’est à dire :
$(x + 1)^2 + (y – 2)^2 = 9$.
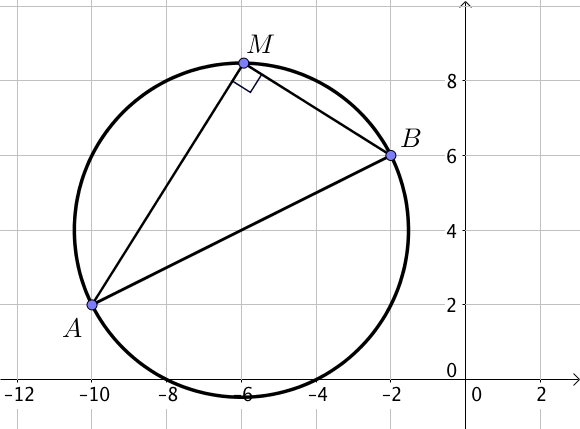
2) Avec le diamètre $[AB]$
Soit $M$ un point du cercle,
alors le triangle $ABM$ est rectangle en $M$ car $[AB]$ est un diamètre du cercle et l’hypoténuse du triangle.
Ainsi, les droites $(MA)$ et $(MB)$ sont perpendiculaires, en d’autres termes, $\overrightarrow{MA} . \overrightarrow{MB} = 0$.
Exemple :
Si $A(-1; 3)$, $B(5; 2)$ et $M(x; y)$ un point appartenant au cercle de diamètre $[AB]$,
Alors une équation cartésienne du cercle se trouve en utilisant la formule $\overrightarrow{MA} . \overrightarrow{MB} = 0$.
$(1 – x)(5 – x) + (3 – y)(2 – y) = 0$
$ x^2 + y^2 -4x -5y + 1 = 0$
C’est une équation cartésienne, qui n’est pas unique.
Il est possible de factoriser cette expression, en remarquant que l’équation contient le début de deux identités remarquables :
$(x – 2)^2 + \left ( y – \dfrac{5}{2} \right )^2 = \dfrac{37}{4}$.
C’est l’équation réduite du cercle qui permet de connaitre le centre du cercle $\Omega\left (2; \dfrac{5}{2} \right)$ et son rayon $\dfrac{\sqrt{37}}{2}$.
Produit scalaire, propriétés
Produit scalaire, propriétés
Définitions
Il existe plusieurs façons de définir le produit scalaire.
1) Avec les coordonnées
Soient $\overrightarrow{u} \left ( \begin{array}{c} x \\ y \\ \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} x’ \\ y’ \\ \end{array} \right )$ deux vecteurs,
le produit scalaire de $\overrightarrow{u}$ scalaire $\overrightarrow{v}$ vaut $\overrightarrow{u} . \overrightarrow{v} = {xx}’ + {yy}’$.
Exemple :
si $\overrightarrow{u} \left ( \begin{array}{c} 2 \\ 3 \\ \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} 4 \\ -1 \\ \end{array} \right )$ alors $\overrightarrow{u} . \overrightarrow{v} = 2 \times 4 + 3 \times (-1) = 5$.
Le résultat d’un produit scalaire n’a pas d’unité.
On prêtera une attention particulière au fait d’utiliser un point pour signifier le produit scalaire entre deux vecteurs.
A partir des coordonnées, il est possible de calculer la norme d’un vecteur, c’est à dire sa longueur : $\| \overrightarrow{u} \| = \sqrt{x^2 + y^2}$.
2) Avec l’angle
On dispose ici de la norme de $\overrightarrow{u}$ notée $\| \overrightarrow{u} \|$ qui correspond à la longueur du vecteur et de la norme de $\overrightarrow{v}$ notée $\| \overrightarrow{v} \|$ ainsi que de l’angle orienté $(\overrightarrow{u}, \overrightarrow{v})$.
Dans ce cas, le produit scalaire vaut : $\overrightarrow{u} . \overrightarrow{v} = \| \overrightarrow{u} \| \times \| \overrightarrow{v} \| \times \cos(\overrightarrow{u}, \overrightarrow{v})$.
Cela permet aussi d’exprimer le cosinus de l’angle : $\cos(\overrightarrow{u}, \overrightarrow{v}) = \dfrac{\overrightarrow{u} . \overrightarrow{v}}{ \| \overrightarrow{u} \| \times \| \overrightarrow{v} \|}$.
Dans certains exercices, on utilisera les coordonnées pour calculer le produit scalaire et la normes des vecteurs et on en déduire à partir de la formule précédente le cosinus de l’angle.
Exemple : Si $\| \overrightarrow{u} \| = 2$, $\| \overrightarrow{v} \| = 3$ et $(\overrightarrow{u}, \overrightarrow{v}) = \dfrac{\pi}{3} (2\pi)$, alors $\overrightarrow{u} . \overrightarrow{v} = 2 \times 3 \times \cos \left ( \dfrac{\pi}{3} \right ) = 3$.
Ainsi, cette formule s’utilise dès lors que l’on connait un angle.
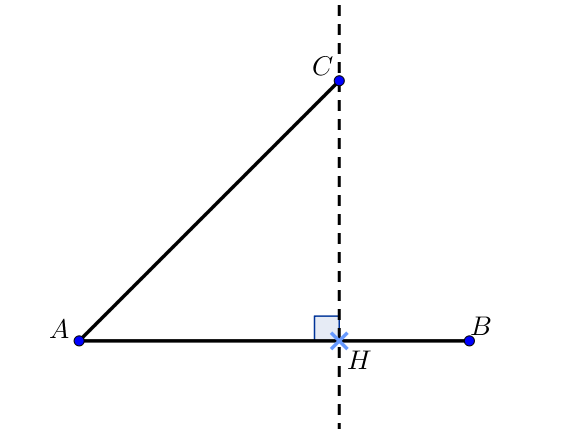
3) Avec le projeté orthogonal
Le projeté orthogonal d’un point sur une droite $(d)$ correspond à l’intersection de la droite perpendiculaire à la droite $(d)$ passant par ce point avec la droite $(d)$.
Soit $H$ le projeté orthogonal de $C$ sur $(AB)$,
alors $ \overrightarrow{AB}.\overrightarrow{AC} = \overrightarrow{AB}.\overrightarrow{AH}$.
Or les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.
Ainsi l’angle les séparant vaut soit 0 soit $\pi$ selon que les vecteurs sont dans le même sens ou dans le sens contraire.
Ainsi, $\overrightarrow{AB}.\overrightarrow{AH}$ sera égal au produit des normes multiplié par $\pm 1$ selon le sens des vecteurs.
4) Autres formules
Il existe deux autres formules moins utilisées permettant de calculer le produit scalaire de $\overrightarrow{u}$ scalaire $\overrightarrow{v}$:
$\overrightarrow{u}. \overrightarrow{v} = \dfrac{1}{2} \left ( \| \overrightarrow{u + v} \|^2 – \| \overrightarrow{u} \|^2 – \| \overrightarrow{v} \|^2 \right )$
$\overrightarrow{u}. \overrightarrow{v} = \dfrac{1}{2} \left (\| \overrightarrow{u} \|^2 + \| \overrightarrow{v} \|^2 -\| \overrightarrow{u – v} \|^2 \right )$
Propriété
Deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul (avec $ \overrightarrow{u} \neq \overrightarrow{0}$ et $\overrightarrow{v} \neq \overrightarrow{0}$).
C’est à dire si $ \overrightarrow{u}. \overrightarrow{v}=0$
Vecteur normal à une droite
Vecteur normal à une droite
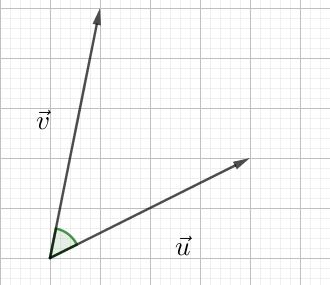
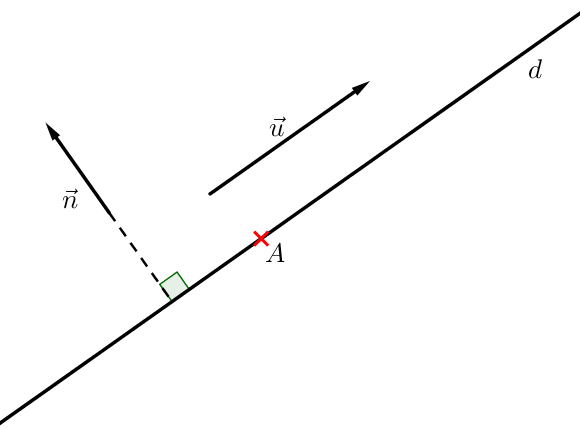
Une droite peut être définie à partir d’un de ses vecteurs directeurs. ($\overrightarrow{u}$ sur la figure)
Elle peut également l’être à partir de l’un de ses vecteurs normaux. ($\overrightarrow{n}$ sur la figure)
Définition :
Un vecteur normal est un vecteur orthogonal à tout vecteur directeur de la droite.
Tout vecteur colinéaire à un vecteur normal est normal à la droite.
Soient $M$ un point quelconque de la droite $(d)$, $A$ un point appartenant à la droite.
Si $\overrightarrow{n}$ est un vecteur normal à cette droite, alors :
$\overrightarrow{AM}.\overrightarrow{n} = 0$.
Vecteur normal et équation cartésienne de droite
On se place dans un repère.
On peut donc écrire les coordonnées des différents éléments précédents :
$\overrightarrow{n} \left ( \begin{array}{c} a \\ b \\ \end{array} \right )$, $M(x; y)$ et $A(x_A; y_A)$.
L’équation $\overrightarrow{AM}.\overrightarrow{n} = 0$ permet de trouver une équation cartésienne de la droite $(d)$ de la forme
$(d) : ax + by + c = 0$, avec $c = -a x_A – b y_A$.
Cette équation cartésienne n’est pas unique à l’inverse de l’équation réduite ($y = ax + b$) qui est unique.
Exemple :
On considère l’équation cartésienne suivante $4x + 2y – 6 = 0$.
D’après le cours, on peut lire les coordonnées d’un vecteur normal $\overrightarrow{n}$ à partir de cette équation : ainsi
$\overrightarrow{n}\left ( \begin{array}{c} 4 \\ 2 \\ \end{array} \right )$.
Un coefficient directeur $\overrightarrow{u}$ d’une droite d’équation réduite $y = ax + b$ est $\overrightarrow{u}\left ( \begin{array}{c} 1 \\ a\\ \end{array} \right )$.
Ainsi, un coefficient directeur de la droite d’équation $y = -2x + 3$ est $\overrightarrow{u}\left ( \begin{array}{c} 1 \\ -2 \\ \end{array} \right )$.