Transformation de l’expression $overrightarrow{MA}cdot overrightarrow{MB}$
Transformation de l'expression $overrightarrow{MA} . overrightarrow{MB}$
Transformation de l’expression $\overrightarrow{MA} . \overrightarrow{MB}$ – Recherche de lieux géométriques
I) Transformation de l’expression $\overrightarrow{MA} . \overrightarrow{MB}$ .
Propriété :
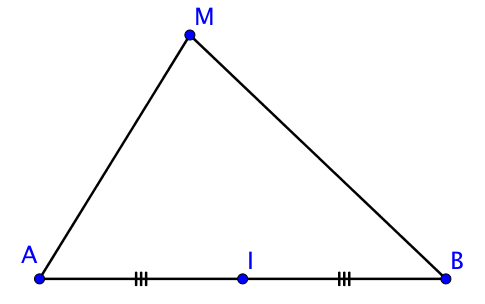
Soient $A$ et $B$ deux points et $I$ milieu de $[AB]$,
Pour tout point $M$ du plan, on a $\overrightarrow{MA} . \overrightarrow{MB} = {MI}^2 – \dfrac{{AB}^2}{4}$.
Rappels :
Le produit scalaire $\overrightarrow{MA} . \overrightarrow{MA}$ peut être calculé de différentes manières.
Il peut être calculé en considérant le produit de la norme de $\overrightarrow{MA}$ par la norme du projeté orthogonal de $\overrightarrow{MA}$ sur lui même, à savoir lui même.
Autrement dit, $\overrightarrow{MA} . \overrightarrow{MA} = MA \times MA = {MA}^2$, où $MA = \| \overrightarrow{MA} \|$.
On peut aussi utiliser la formule faisant intervenir le cosinus de l’angle orienté entre les deux vecteurs :
$\overrightarrow{MA} . \overrightarrow{MA} = MA \times MA \times \cos(\overrightarrow{MA};\overrightarrow{MA})$.
Or $(\overrightarrow{MA};\overrightarrow{MA}) = 0$ et comme $\cos(0) = 1$ alors $\overrightarrow{MA} . \overrightarrow{MA} = MA \times MA = {MA}^2$.
On a ainsi l’égalité suivante : $\overrightarrow{MA}^2 = \overrightarrow{MA} . \overrightarrow{MA} = {MA}^2$.
Preuve de la propriété :
On calcule le produit scalaire $\overrightarrow{MA} . \overrightarrow{MB}$ en utilisant le point $I$ et la relation de Chasles :
$\overrightarrow{MA} . \overrightarrow{MB} = (\overrightarrow{MI} + \overrightarrow{IA}) . (\overrightarrow{MI}+ \overrightarrow{IB})$.
Or $I$ est le milieu de $[AB]$ donc $\overrightarrow{AI} = \overrightarrow{IB} =- \overrightarrow{IA} $.
Ainsi, $\overrightarrow{MA} . \overrightarrow{MB} = (\overrightarrow{MI} + \overrightarrow{IA}) . (\overrightarrow{MI}- \overrightarrow{IA}) = \overrightarrow{MI}^2 – \overrightarrow{IA}^2 = {MI}^2 – {IA}^2$.
Enfin, comme $I$ est le milieu de $[AB]$ on peut écrire que $IA = \dfrac{AB}{2}$.
Ansi, $\overrightarrow{MA} . \overrightarrow{MB} = {MI}^2 – \left ( \dfrac{AB}{2} \right )^2 = {MI}^2 – \dfrac{{AB}^2}{4}$.
II) Recherche de lieux géométriques
Exemple :
Soient $A$ et $B$ deux points tels que $AB = 4$ cm.
On cherche à déterminer l’ensemble des points $M$ tels que $\overrightarrow{MA} . \overrightarrow{MB} = 12$.
On applique la propriété précédente pour trouver cet ensemble de points.
$\overrightarrow{MA} . \overrightarrow{MB} = 12$
$\iff {MI}^2 – \dfrac{{AB}^2}{4} = 12$
$\iff {MI}^2 – \dfrac{4^2}{4} = 12$
$ \iff {MI}^2 – 4 = 12$
$ \iff {MI}^2= 16$.
Comme $MI$ est une distance, la solution de cette équation est un nombre positif, ainsi :
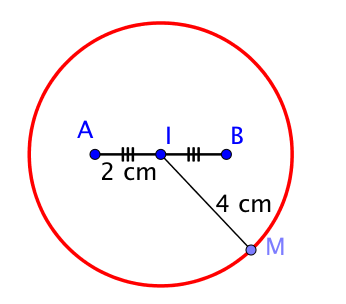
$MI = 4$.
Cela correspond donc à l’ensemble des points $M$ situés à une distance de $4$ centimètres du point $I$, il s’agit donc du cercle de centre $I$ et de rayon $4$.