Théorème du toit
Théorème du toit
Théorème du toit
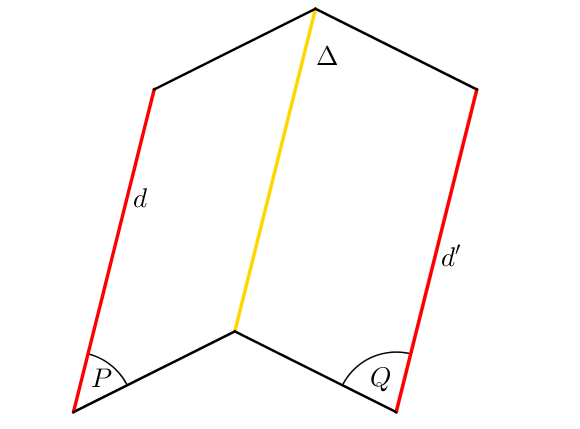
La configuration des deux plans forme un toit, ce qui explique le nom de ce théorème.
Théorème :
Soient $P$ et $Q$ deux plans de l’espace sécants selon la droite $\Delta$,
Soit $d$ une droite de $(P)$
$d’$ une droite de $(Q)$
Si $d\ // \ d’$ alors $d\ // \ \Delta \ // \ d’$.
Ce théorème permet de montrer que des droites sont parallèles :
Si deux droites sont parallèles dans deux plans sécants, alors ces droites sont parallèles à la droite d’intersection des deux plans.