Fonction cube
La fonction cube
Définition
Soit $f$ la fonction cube définie pour tout $x \in \mathbb{R}$ par $f(x) = x^3$.
Exemples
Calculons quelques valeurs de la fonction.
$f(0) = 0^3 = 0 \times 0 \times 0 = 0$.
$f(-2) = (-2)^3 = (-2) \times (-2) \times (-2) = 4 \times (-2) = -8$.
$f \left (\dfrac{2}{3} \right ) = \left (\dfrac{2}{3} \right ) ^3 = \dfrac{8}{27}$.
Signe et variations
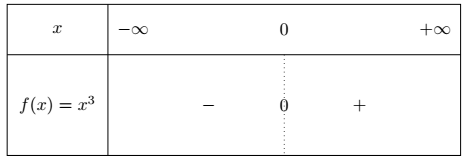
$f$ est négative lorsque $x$ est négatif et positive lorsque $x$ est positif.
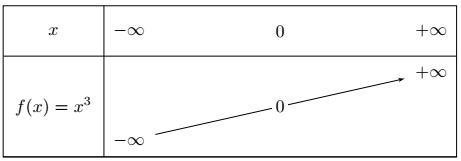
Tableau de variation :
La fonction cube est croissante.
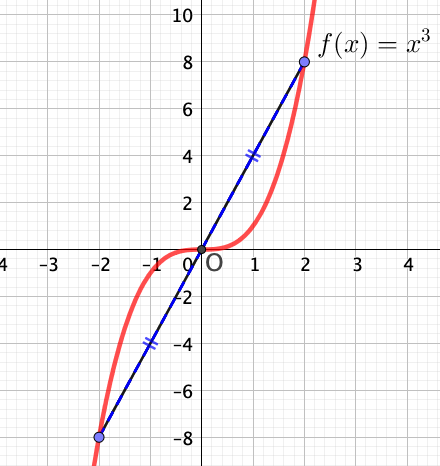
La courbe de la fonction cube est la suivante.
Propriétés
Soit $x \in \mathbb{R}$,
on calcule l’image de l’opposé de $x$:
$f(-x) = (-x)^3 = (-x) \times (-x) \times (-x) = x^2 \times (-x) = – x^3 = -f(x)$.
Ainsi $f(-x) = – f(x)$.
On dit alors que la fonction $f$ est impaire.
Ainsi la courbe de $f$ est symétrique par rapport à l’origine.
Positions relatives de courbes usuelles.
La position relative de la fonction cube par rapport aux fonctions $g(x) = x$ et $h(x) = x^2$ doit être connue.
Pour cela on étudie le signe de la différence de $f$ et de $g$ puis de $f$ et de $h$, en cherchant à factoriser l’expression pour faciliter l’étude du signe.
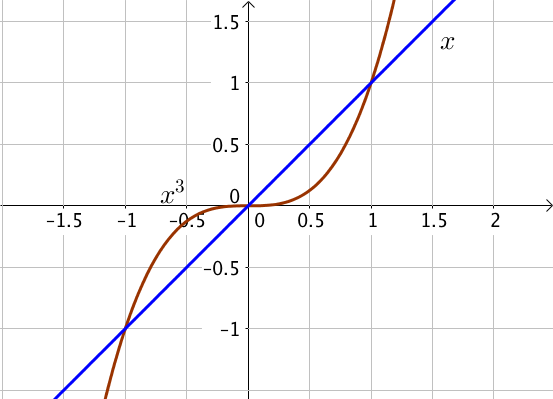
Position relative avec $g(x)= x$
Soit $x \in \mathbb{R}$,
$f(x) – g(x) = x^3 – x = x(x^2 -1) = x(x – 1)(x + 1)$.
On réalise donc le tableau de signe pour chaque facteur du produit, puis on utilise la règle des signes du produit pour trouver le signe de la différence.
On trouve ainsi que $f(x) – g(x) < 0$ pour $x \in ]-\infty; -1[$ et $]0;1[$, ainsi $f$ est inférieure à $g$ sur ces intervalles et donc la courbe de $f$ est en dessous de celle de $g$ pour ces intervalles.
On trouve ainsi que $f(x) – g(x) > 0$ pour $x \in ]-1; 0[$ et $]1; +\infty[$, ainsi $f$ est supérieure à $g$ sur ces intervalles et donc la courbe de $f$ est au dessus de celle de $g$ sur ces intervalles.
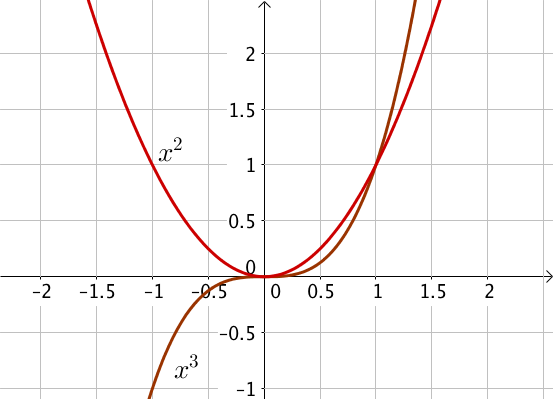
Position relative avec $h(x)= x^2$
Soit $x \in \mathbb{R}$,
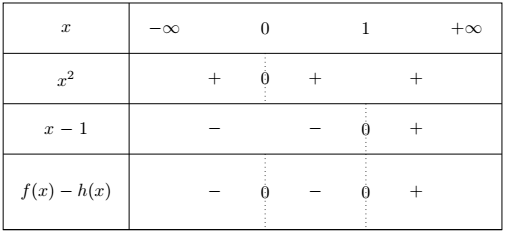
$f(x) – h(x) = x^3 – x^2 = x^2(x -1) $.
On réalise donc le tableau de signe pour chaque facteur du produit, puis on utilise la règle des signes du produit pour trouver le signe de la différence.
On trouve ainsi que $f(x) – h(x) < 0$ pour $x \in ]-\infty; 0[$ et $]0;1[$, ainsi $f$ est inférieure à $h$ sur ces intervalles et donc la courbe de $f$ est en dessous de celle de $h$ pour ces intervalles.
On trouve ainsi que $f(x) – h(x) > 0$ pour $]1; +\infty[$, ainsi $f$ est supérieure à $h$ sur cet intervalle et donc la courbe de $f$ est au dessus de celle de $g$ sur cet intervalle.