Translations

Translations

Translations

Les translations sont des transformations du plan. Une translation correspond à un glissement. 

Définition 

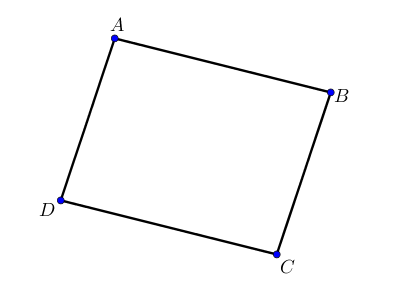
Soit $ABCD$ un parallélogramme.

La translation qui transforme $A$ en $B$ transforme aussi $D$ en $C$.  

Propriétés

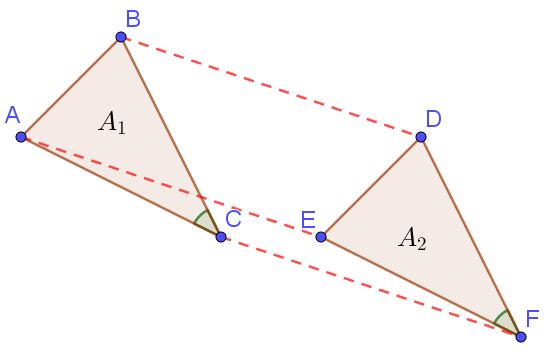
Les translations conservent les longueurs, les aires et les mesures d’angles : il n’y a pas de déformations de figure lors d’une translation. 

Dans cette figure la translation qui transforme $B$ en $D$ transforme le triangle $BCA$ en $DFE$

$AB=DE$  ; $AC=EF$   et $BC=DF$

Ces deux triangles ont les mêmes aires $A_1=A_2$

Les angles$\widehat{BCA}$ et $\widehat{DFE}$ ont la même mesure.