Variations de fonctions
Variations de fonctions
Propriété :
Soit $f$ une fonction dérivable sur $I$,
si pour tout $x \in I$, la dérivée est strictement positive alors la fonction $f$ est strictement croissante sur $I$.
si pour tout $x \in I$, la dérivée est strictement négative alors la fonction $f$ est strictement décroissante sur $I$.
Pour étudier les variations d’une fonction, on commence par calculer la dérivée de la fonction puis on étudie le signe de la dérivée.
On conclut enfin sur les variations de la fonction.
Exemple :
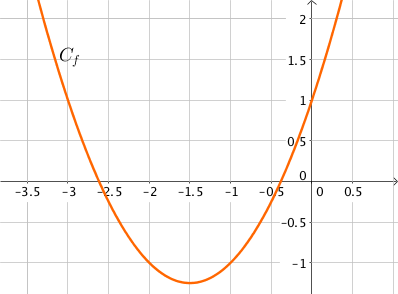
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = x^2 + 3x + 1$ et dérivable sur $\mathbb{R}$.
On souhaite étudier les variations de la fonction $f$.
La dérivée de la fonction $f$ est $f'(x) = 2x + 3$.
On étudie le signe de la dérivée :
$f'(x) > 0 \iff 2x + 3 > 0 \iff x > \dfrac{-3}{2}$
De même, $ f'(x) < 0 \iff x < \dfrac{-3}{2}$.
On peut alors remplir le tableau de signe de la dérivée.
Pour $x \in ]- \infty; -\frac{3}{2}[$, la dérivée est strictement négative, la fonction $f$ est donc strictement décroissante sur cet intervalle.
Pour $x \in ]-\frac{3}{2}, + \infty; [$, la dérivée est strictement positive, la fonction $f$ est donc strictement croissante sur cet intervalle.
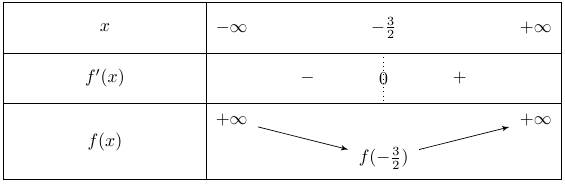
Une flèche vers le haut symbolise une fonction croissante alors qu’une flèche vers le bas marque une fonction décroissante.
On indique également aux extrémités des flèches la valeur de la fonction au point correspondant lorsque l’on peut la calculer.
On obtient alors le tableau de variations de la fonction $f$ suivant que l’on écrit sous le tableau de signe :
On remarque que la fonction $f$ admet un minimum atteint en $x = – \dfrac{3}{2}$ ce qui correspond à $x = \dfrac{-b}{2a}$ lorsque le polynôme du second degré s’écrit $ax^2 + bx + c$.
Le tableau de variation permet donc d’étudier les extrema d’une fonction.