Centre de gravité du triangle
Centre de gravité d’un triangle
Rappel : milieu d’un segment
Soient $B$ et $C$ deux points du plan,
$A’$ est le milieu de $[BC]$ si et seulement si $\overrightarrow{BA’} = \dfrac{1}{2} \overrightarrow{BC}$ ce qui est équivalent à dire en utilisant la relation de Chasles que $\overrightarrow{A’B} + \overrightarrow{A’C}= \overrightarrow{0}$
Définition :
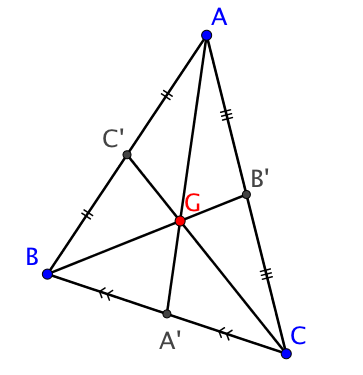
Soit $ABC$ un triangle, il existe un point du plan, noté $G$, et un seul, tel que
$\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}$.
Ce point est appelé le centre de gravité du triangle.
1. Point de concours des médianes
On réécrit cette égalité en faisant apparaitre le point $A$ dans les deux derniers vecteurs par la relation de Chasles.
Cela devient alors
$\overrightarrow{GA} + (\overrightarrow{GA} + \overrightarrow{AB}) + (\overrightarrow{GA} + \overrightarrow{AC}) = \overrightarrow{0}$
En regroupant les $\overrightarrow{GA}$ on a alors :
$\overrightarrow{AG} = \dfrac{1}{3} (\overrightarrow{AB} + \overrightarrow{AC})$
Enfin, en faisant apparaitre le milieu de $[BC]$, c’est à dire $A’$ on trouve :
$\overrightarrow{AG} = \dfrac{1}{3} (\overrightarrow{AA’} + \overrightarrow{A’C} + \overrightarrow{AA’} + \overrightarrow{A’B}) = \dfrac{2}{3} \overrightarrow{AA’} + \dfrac{1}{3}(\overrightarrow{A’C}+ \overrightarrow{A’B}) $
Or $(\overrightarrow{A’C}+ \overrightarrow{A’B})$ par définition car $A’$ est le milieu du segment.
On obtient ainsi une propriété importante :
$\overrightarrow{AG} = \dfrac{2}{3} \overrightarrow{AA’}$.
De même, on trouve :
$\overrightarrow{BG} = \dfrac{2}{3} \overrightarrow{BB’}$
$\overrightarrow{CG} = \dfrac{2}{3} \overrightarrow{CC’}$.
Cela signifie donc que le point $G$ est situé au $ \dfrac{2}{3}$ des médianes du triangle en partant des sommets.
Il appartient donc aux trois médianes du triangle, qui sont concourantes en un seul point : c’est donc le centre de gravité $G$.
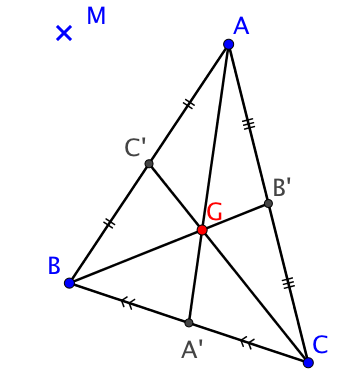
2. Valeur minimale de ${MA}^2 + {MB}^2 + {MC}^2 $
Soit $ABC$ un triangle et $G$ son centre de gravité.
A tout point $M$ du plan on associe le réel ${MA}^2 + {MB}^2 + {MC}^2 $
Par exemple, si $M = A$, on obtient l’égalité suivante : ${MA}^2 + {MB}^2 + {MC}^2 = {AB}^2 + {AC}^2 $.
On cherche à présent le point $M$ rendant minimal le réel $f(M) = {MA}^2 + {MB}^2 + {MC}^2 $.
Or ${MA}^2 = \overrightarrow{MA}^2$. On réécrit donc la fonction $f$ en écrivant des vecteurs.
$f(M) = \overrightarrow{MA}^2 + \overrightarrow{MB}^2 + \overrightarrow{MC}^2$
On applique à présent la propriété de Chasles en introduisant le point $G$ :
$f(M) = (\overrightarrow{MG} + \overrightarrow{GA})^2 + (\overrightarrow{MG} + \overrightarrow{GB})^2 + (\overrightarrow{MG} + \overrightarrow{GC})^2$
On peut ensuite appliquer les formules de développement des identités remarquables.
Donc, $f(M) = 3\overrightarrow{MG}^2 + \overrightarrow{GA}^2 + \overrightarrow{GB}^2 +\overrightarrow{GC}^2 + 2\overrightarrow{MG}.(\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC})$
Or par définition, $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}$
Ainsi, $f(M) = 3\overrightarrow{MG}^2 + \overrightarrow{GA}^2 + \overrightarrow{GB}^2 +\overrightarrow{GC}^2 $
La quantité $\overrightarrow{GA}^2 + \overrightarrow{GB}^2 +\overrightarrow{GC}^2 $ est fixe, seul le terme $3{MG}^2$ est variable.
De plus, $3{MG}^2 \geq 0$, donc en ajoutant $\overrightarrow{GA}^2 + \overrightarrow{GB}^2 +\overrightarrow{GC}^2 $ des deux côtés on trouve :
$f(M) \geq \overrightarrow{GA}^2 + \overrightarrow{GB}^2 +\overrightarrow{GC}^2 $
On vient de trouver un minorant de la fonction $f$.
Il reste à déterminer si il existe une valeur de $M$ pour laquelle la fonction $f$ est égale à ce minorant qui serait alors le minium de la fonction.
On remarque que $f(M) = \overrightarrow{GA}^2 + \overrightarrow{GB}^2 +\overrightarrow{GC}^2 $ lorsque le terme $3{MG}^2$ est nul, ou encore que $GM = 0$ ce qui signifie que $M = G$.
Conclusion :
La fonction $f$ est minimale lorsque $M$ est confondu avec le centre de gravité $G$ et elle vaut alors ${GA}^2 + {GB}^2 + {GC}^2$.