Médiane
Médiane d’une série statistique
Définition
La médiane $m$ d’une série statistique est une valeur du caractère étudiée telle que la moitié de la population a des valeurs inférieures à $m$ et l’autre moitié des valeurs supérieures à $m$.
Calcul pratique :
Pour trouver la médiane, il faut commencer par classer les valeurs par ordre croissant.
Il faut ensuite distinguer deux cas selon la parité de l’effectif total (le nombre d’individus dans la population) de la série.
1e cas : l’effectif total $N$ est pair
La médiane est la moyenne des valeurs de rang $\dfrac{N}{2}$ et $\dfrac{N}{2} + 1$.
Exemple : on considère un effectif total $N = 6$. La médiane est donc la moyenne de la troisième valeur et de la quatrième.
2e cas : l’effectif total $N$ est impair.
La médiane est la valeur de rang $\dfrac{N + 1}{2}$.
Exemple
Considérons la série statistique suivante donnant un relevé de notes dans un groupe d’élèves:
| Notes | 6 | 7 | 8 | 10 | 12 |
| Effectifs | 2 | 3 | 4 | 5 | 3 |
L’effectif total est $N = 17$. L’effectif total est impair.
La série statistique est ordonnée dans l’ordre croissant.
La médiane sera donc la valeur de rang $\dfrac{N +1}{2} = \dfrac{17 + 1}{2} = 9$.
On cherche ainsi la neuvième valeur en additionnant les effectifs.
| Notes | 6 | 7 | 8 | 10 | 12 |
| Effectifs | 2 | 3 | 4 | 5 | 3 |
| Effectifs cumulés croissants | 2 | 5 | 9 | 14 | 17 |
Ainsi, 5 personnes ont eu moins de 7.
De même, 9 personnes ont eu moins de 8.
Ainsi, la neuvième note est 8.
La médiane est donc 8.
Cela signifie donc que sur l’effectif total, la moitié des personnes a eu une note inférieure à 8 alors que l’autre moitié a eu une note supérieure à 8.
Il existe une autre méthode pour trouver la médiane qui consiste à expliciter la série statistique : il y a donc deux 6 puis trois 7 puis quatre 8 et ainsi de suite… Puis on compte jusqu’à la neuvième note.
La moyenne et la médiane sont deux indicateurs statistiques différents.
Quartiles
Quartiles d’une série statistique
Définition
Le premier quartile noté $Q_1$ est le plus petit élément des valeurs des termes de la série statistique tel qu’au moins 25% des données sont inférieures ou égales à $Q_1$.
Le troisième quartile noté $Q_3$ est le plus petit élément des valeurs des termes de la série statistique tel qu’au moins 75% des données sont inférieures ouégales à $Q_3$.
Méthodes de calculs :
On commence par ordonner par ordre croissant la série statistique puis on détermine l’effectif total $N$.
Afin de trouver la valeur du premier quartile, on calcule $\dfrac{N}{4}$.
Si le résultat est un entier, $Q_1$ sera la valeur de rang $\dfrac{N}{4}$.
Exemple : si $N = 16$, alors $Q_1$ est la quatrième valeur de la série.
Si le résultat n’est pas un entier, $Q_1$ est la valeur dont le rang est le premier entier supérieur à $\dfrac{N}{4}$.
Exemple : si $N = 21$, alors $Q_1$ est la sixième valeur de la série.
Pour trouver la valeur du troisième quartile, on applique la même méthode en calculant $\dfrac{3N}{4}$.
Exemple :
Considérons la série de notes suivante :
| Notes | 6 | 7 | 8 | 10 | 12 |
| Effectifs | 2 | 3 | 4 | 5 | 3 |
La série est classée par ordre croissant.
L’effectif total est $N = 17$.
On calcule alors $\dfrac{N}{4} = \dfrac{17}{4} = 4,25$.
Le résultat n’est pas un entier, ainsi $Q_1$ est la valeur dont le rang est le premier entier supérieur à 4,25 c’est à dire 5.
Donc $Q_1$ est la cinquième note : $Q_1 = 7$.
On calcule de même $\dfrac{3N}{4} = \dfrac{3 \times 17}{4} =12,75$.
Le résultat n’est pas un entier, ainsi $Q_3$ est la valeur dont le rang est le premier entier supérieur à 12,75 c’est à dire 13.
Donc $Q_3$ est la treizième note : $Q_3 = 10$.
La calculatrice dispose d’outils permettant d’effectuer le calcul des quartiles.
Diagrammes en boîte et écart intercartile
Diagrammes en boîte et écart interquartile
Définition
Le diagramme en boîte est un schéma qui résume la série statistique.
Pour le construire, il faut avoir calculer au préalable la médiane et les quartiles.
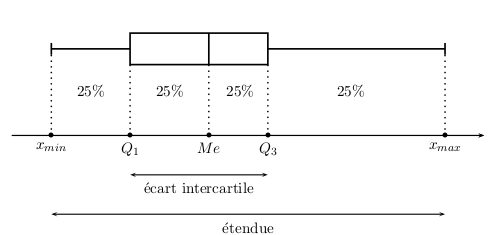
Les valeurs minimale et maximale de la série sont placées aux extrémités du diagramme.
Entre ces deux valeurs est placé un rectangle dont la première largeur correspond au premier quartile et la largeur opposée au troisième quartile.
Le segment contenu dans le rectangle correspond à la médiane.
L’écart interquartile correspond à la différence entre le troisième quartile et le premier, il est donc égal à $Q_3 – Q_1$.
L’intervalle interquartile est l’intervalle ayant pour bornes les quartiles, c’est à dire $[Q_1; Q_3]$. Il est visible sur le diagramme en boîte.
Exemple :
Considérons la série statistique suivante représentant les notes d’élèves :
| Notes | 6 | 7 | 8 | 10 | 12 |
| Effectifs | 2 | 3 | 4 | 5 | 3 |
La médiane de cette série statistique est 8, le premier quartile est 7 et le troisième vaut 10.
Pour construire le diagramme en boîte associé, on commence par construire l’axe gradué correspond aux valeurs de la série.
On place donc le premier côté du rectangle pour une valeur égale à 7 puis on place un autre côté du rectangle pour une valeur de 10.
On place ensuite les valeurs minimale et maximales de la série.
Enfin, on place la valeur de la médiane à l’intérieur du rectangle.
Interprétations
Le diagramme est donc un outil visuel permettant de faire de nombreuses interprétations.
Par exemple, on peut voir que 50% des élèves a eu une note inférieure à 8. D’autre part, 25% des élèves a eu une note supérieure à 10.
En outre, la moitié de la population est comprise dans le rectangle, donc la moitié des notes est comprise entre 7 et 10.


