Équations de droites - Définition
Équations de droites
Définition:
On se place dans le plan muni d’un repère.
Toute droite du plan possède une équation de la forme :
$x = k$ si il s’agit d’une droite parallèle à $(Oy)$, où $k$ est un réel
$y = ax + b$ si il s’agit d’une droite sécante à $(Oy)$ : c’est l’équation réduite de la droite.
$a$ est un réel correspondant au coefficient directeur de la droite, il donne l’inclinaison de la droite.
$b$ est un réel correspondant à l’ordonnée à l’origine, c’est à dire l’ordonnée du point d’intersection de la droite avec l’axe des ordonnées.
Exemple :
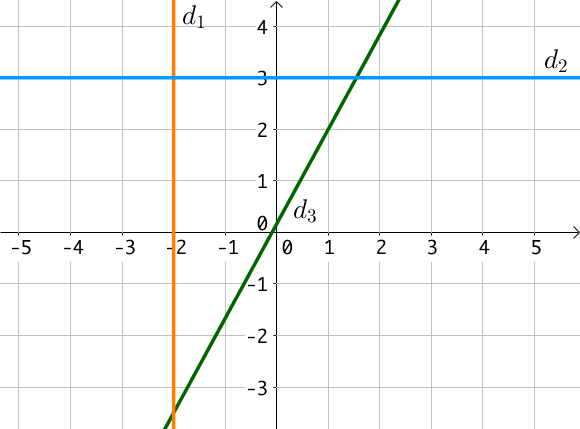
La droite $(d_1)$ est parallèle à l’axe des ordonnées. Son équation est donc de la forme $x = k$. Ainsi $k$ correspond à la valeur de l’abscisse. Tous les points de la droite ont même abscisse : $-2$, alors que leurs ordonnées sont variables. Ainsi, $x = -2$.
Un point quelconque appartenant à la droite $(d_2)$ a pour ordonnée 3, et une abscisse quelconque : l’équation réduite de cette droite est donc $y = 3$. Il s’agit d’une équation réduite car on peut écrire cette équation comme $y = 0\times x + 3$.
La droite $(d_3)$ a une équation de la forme $y = ax + b$ mais il n’est pas possible de déterminer $a$ et $b$ car on ne dispose d’aucune donnée pour cette droite. Il faudrait au moins les coordonnées de deux points.
Droites parallèles
Considérons deux droites $(\Delta)$ et $(\Delta ‘)$ d’équations réduites :
$\Delta : y = ax+b$
$\Delta’ : y = a’x+b’$
Les droites $(\Delta)$ et $(\Delta ‘)$ sont parallèles si et seulement si elles ont le même coefficient directeur,
Autrement dit $(\Delta) // (\Delta ‘) \iff a =a’$
Si les deux droites ont une équation de la forme
$\Delta : x = k$
$\Delta’ : x = k’$
alors elles sont parallèles.
Tracer des droites d'équations données
Tracer des droites d’équations données
On souhaite tracer les équations de droites suivantes :
$d_1 : y = -2 \\
d_2 : x = 3 \\
d_3 : y = -\dfrac{1}{3}x + 2 \\
d_4 : y = 2x – 2$
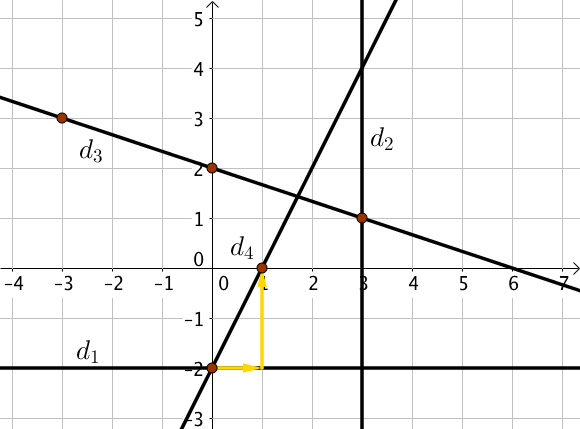
$(d_1)$ est une droite horizontale, de coefficient directeur nul. On trace donc la droite parallèle à l’axe des abscisses passant par le point $(0; -2)$.
$(d_2)$ est une droite verticale, parallèle à l’axe des ordonnées et passant par le point de coordonnées $(3; 0)$.
Pour tracer les droites $(d_3)$ et $(d_4)$, il existe deux méthodes.
La première consiste à dresser un tableau de valeurs, en général on prendra 3 points. 2 points suffisent pour tracer une droite, mais il est bon de prendre la précaution d’en placer 3 pour éviter les erreurs.
On choisit donc différentes valeurs de $x$ et on remplace ces valeurs dans l’équation de la droite $(d_3)$ pour obtenir la valeur de $y$ correspondante.
On peut aussi remarquer que le coefficient directeur vaut $-\dfrac{1}{3}$, ainsi en prenant des valeurs de $x$ multiples de 3, on trouve des valeurs de $y$ entières.
| $x$ | $-3$ | $0$ | $3$ |
| $y$ | $3$ | $2$ | $1$ |
Le coefficient directeur étant un nombre négatif, la droite “descend”.
Pour tracer la droite $(d_4)$, on utilise la seconde méthode.
On utilise l’ordonnée à l’origine qui vaut $-2$. Le point $(0; -2)$ appartient donc à la droite.
On utilise ensuite le coefficient directeur : on se déplace d’une unité vers la droite depuis l’ordonnée à l’origine puis on se déplace verticalement avec un nombre d’unités égale au coefficient directeur (on se déplacera vers le haut pour un coefficient positif et vers le bas pour un coefficient négatif).
Ici, on se déplace de deux unités vers le haut.
On obtient ainsi un second point appartenant à la droite, en reliant ces deux points on obtient donc la droite $(d_4)$.
Déterminer une équation de droite
Déterminer une équation de droite
Méthode
Pour déterminer l’équation d’une droite, deux points appartenants à cette droite sont généralement donnés.
Soient donc deux points $A(x_A; y_A)$ et $B(x_B; y_B)$.
La notation $x_A$ signifie abscisse du point $A$ et $y_A$ signifie ordonnée du point $A$.
La droite $(AB)$ a pour coefficient directeur
$a = \dfrac{y_B – y_A}{x_B – x_A}$.
Cette formule est vraie lorsque les points $A$ et $B$ n’ont pas la même abscisse, sinon il s’agit d’une droite verticale qui n’admet pas de coefficient directeur.
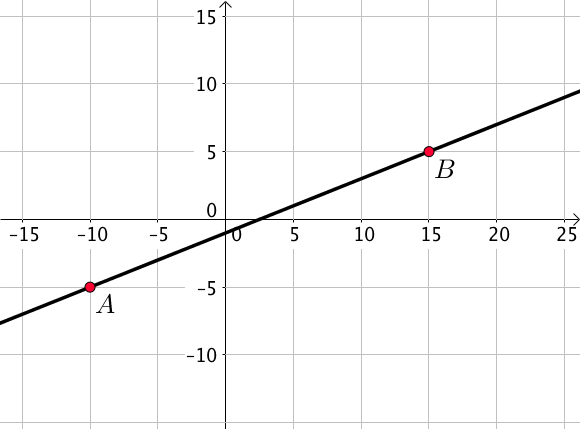
Considérons par exemple les points $A(-10; -5)$ et $B(15; 5)$ représentés sur le schéma ci dessous.
1) On cherche ici une équation du type $y = ax + b$.
On utilise donc la propriété pour trouver la valeur de $a$ :
$a =\dfrac{y_B – y_A}{x_B – x_A}=\dfrac{5 – (-5)}{15 – (-10)} = \dfrac{10}{25} = \dfrac{2}{5}$.
On veillera à bien utiliser des parenthèses.
Ainsi, $y = \dfrac{2}{5}x + b$, il faut maintenant trouver la valeur de $b$.
2) On sait que $A \in (AB)$ donc les coordonnées du point $A$ vérifient l’équation de la droite.
Ainsi $y_A = \dfrac{2}{5} x_A + b$ ou encore $-5 = \dfrac{2}{5} \times (-10) + b$.
C’est une équation à une inconnue que l’on résout.
$-5 = -4 + b$
$-1 = b$
Finalement, $(AB) : y = \dfrac{2}{5}x – 1$.
Points alignés
Points alignés
Deux points étant toujours alignés, on considérera trois points ou plus dans la suite.
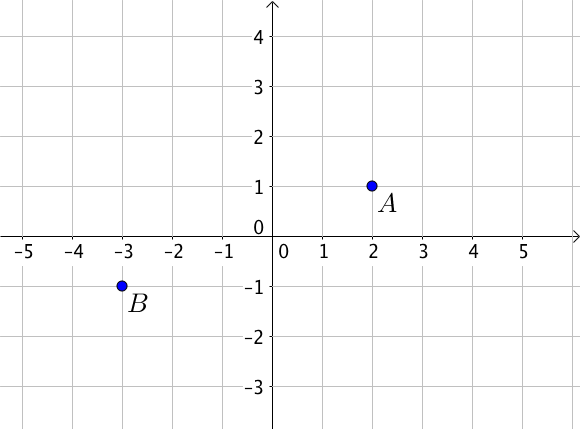
Soient trois points $A(2;1), B(-3; -1)$ et $C(12; 5)$,
On se contente de représenter uniquement les points $A$ et $B$.
Les points $A, B$ et $C$ sont ils alignés ?
Méthode :
Pour répondre à cette question, la méthode consiste à calculer le coefficient directeur de la droite $(AB)$ puis le coefficient de la droite $(AC)$.
Or si ces coefficients directeurs sont égaux, alors les deux droites sont parallèles.
Mais ces deux droites possèdent alors un point commun : $A$, les deux droites sont donc confondues : les points sont donc alignés.
Il faut donc commencer par calculer les deux coefficients directeurs.
Le coefficient directeur de la droite $(AB)$ est :
$a =\dfrac{y_B-Y_A}{x_B-x_A}=\dfrac{-1 -1}{-3 – 2} = \dfrac{2}{5}$.
Le coefficient directeur de la droite $(AC)$ est :
$a’ =\dfrac{y_C-Y_A}{x_C-x_A}= \dfrac{5 -1}{12 – 2} = \dfrac{4}{10} = \dfrac{2}{5}$.
Ainsi $a = a’$, les droites $(AB)$ et $(AC)$ sont donc parallèles et ont un point commun : les points $A, B$ et $C$ sont alignés.
Le fait de tracer une droite reliant les trois points ne prouve pas l’alignement.


