Pourcentages
Pourcentages
I – Pourcentages instantanés
1) Déterminer un pourcentage
Lorsque l’on connait l’effectif total d’un groupe et l’effectif d’une partie du groupe, on peut déterminer la proportion que cette partie du groupe représente par rapport à l’ensemble qui vaut alors
$\text{Proportion } = \dfrac{\text{Effectif partie}}{\text{Effectif total}}$.
Le pourcentage associé vaut alors : $\text{Pourcentage } = \dfrac{\text{Effectif partie}}{\text{Effectif total}} \times 100$
Exemple :
Dans une classe de seconde de 35 élèves, il y a 14 garçons.
La proportion de garçons est $\dfrac{14}{35} = \dfrac{2}{5}$.
Le pourcentage de garçons est alors de $\dfrac{14}{35} \times 100= 40 \%$.
2) Déterminer l’effectif d’une partie
Lorsque l’on connait le pourcentage d’une partie d’un ensemble et l’effectif total de cet ensemble, on peut alors déterminer l’effectif de la partie associée.
On a alors $\text{Effectif partie} = \text{Proportion} \times \text{Effectif total} = \dfrac{\text{Pourcentage}}{100} \times \text{Effectif total}$.
Exemple :
Dans un lycée, il y a 200 élèves de seconde.
15% des élèves de seconde font du Latin.
On cherche à exprimer le nombre d’élèves latinistes.
$\dfrac{15}{100} \times 200 = 0,15 \times 200 = 30$.
Il y a donc 30 élèves latinistes de seconde.
3) Déterminer l’effectif total
On connait l’effectif de la partie et le pourcentage de cette dernière, pour déterminer l’effectif total on applique la formule :
$\text{Effectif total} = \dfrac{\text{Partie} \times 100}{\text{Pourcentage}}$.
On peut s’aider du tableau de proportionnalité suivant :
| Pourcentage | Effectif de la partie |
| 100% | Effectif total |
Exemple :
Dans une classe, il y a 12 germanistes qui représentent 40% du groupe.
Le nombre d’élèves dans cette classe est alors donné par la formule $\dfrac{12 \times 100}{40} = 30$.
4) Pourcentage de pourcentage
L’effectif total est connu. On considère un groupe de l’ensemble que l’on note $B$ et un sous groupe de ce groupe que l’on appelle $A$.
$A$ représente $a \%$ de $B$.
$B$ représente $b \%$ du total.
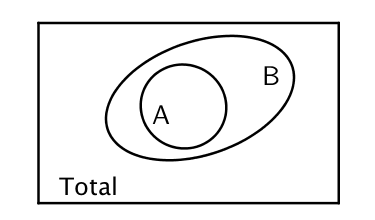
$A$ représente alors $a \%$ de $b \%$ de l’effectif total.
La formule associée est donc $\dfrac{a \times b}{100} \%$ de l’effectif total.
Exemple :
Dans une classe, il y a $45 \%$ de garçons dont $80 \%$ ont moins de 18 ans.
Le pourcentage de garçons de moins de 18 ans dans la classe est donc de $\dfrac{45\times 80}{100} = 36 \%$.


