Proportionnalité
Proportionnalité
Définition
Il y a proportionnalité dans un tableau, lorsque les termes d’une ligne s’obtiennent en multipliant ou en divisant par un même nombre ceux de l’autre ligne.
Ce nombre est le coefficient de proportionnalité.
Exemple :
- Tableau 1
|
3 |
1 |
1.5 |
|
18 |
6 |
9 |
Dans le premier tableau, on passe de la première à la deuxième ligne en multipliant par 6.
C’est une situation de proportionnalité et le coefficient de proportionnalité vaut 6.
- Tableau 2
| 4 | 8 | 6 |
| 10 | 20 | 30 |
Dans le second tableau,
$10\div 4= 2,5$
$20\div 8= 2,5$ mais
$30\div 6= 5$
Ce n’est donc pas une situation de proportionnalité.
Dans la vie quotidienne
A la pompe à essence, on peut acheter du Sans plomb 95 valant 1,45 euros le litre.
Les deux grandeurs proportionnelles qui interviennent sont : le volume d’essence en Litre (L) et le prix en euros (€)
Le coefficient de proportionnalité vaut 1,45.
|
Volume d’essence (L) |
1 |
2 |
3 |
12 |
|
Prix (euros) |
1,45 |
2,90 |
4,35 |
17,40 |
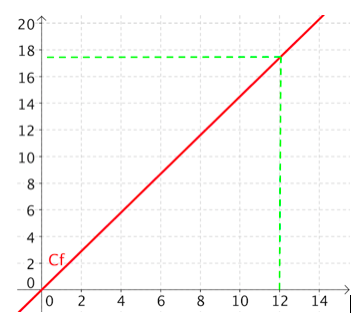
Représentation graphique :
Commentaire :
La représentation graphique d’une situation de proportionnalité est toujours une droite passant par l’origine.
On dira ici que le prix est proportionnel au volume d’essence.
Attention ! il n’en va pas toujours ainsi : Par exemple, le poids d’un enfant n’est pas proportionnel à sa taille.