Point d’inflexion
Point d’inflexion
I. Définition du point d’inflexion
Qu’est-ce qu’un point d’inflexion ?
Un point d’inflexion d’une courbe est un point où la courbe traverse sa tangente.
Il s’agit d’une définition visuelle.
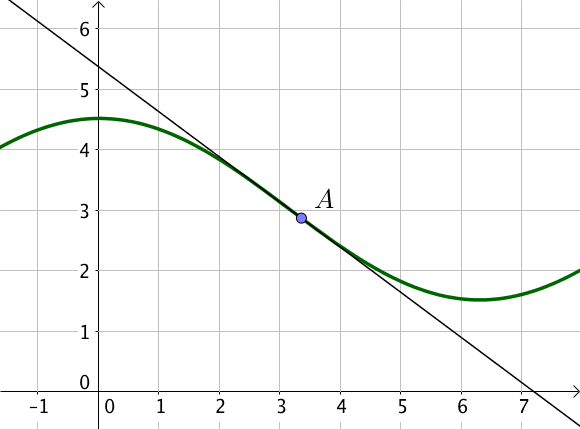
L’exemple qui suit représente un point d’inflexion au point $A$ car la courbe traverse sa tangente au point $A$ : elle est d’abord en dessous de sa tangente qui croise sa tangente au point $A$ et passe au dessus ensuite.
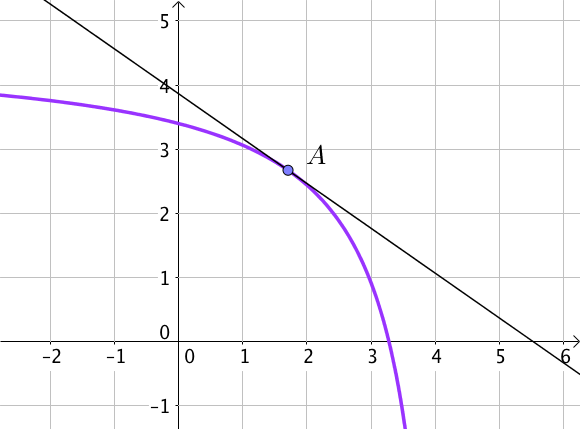
L’exemple ci-dessous montre que $A$ n’est pas un point d’inflexion : la courbe ne traverse pas sa tangente au point $A$ et reste toujours en dessous de cette dernière.
II. Exemple à connaître
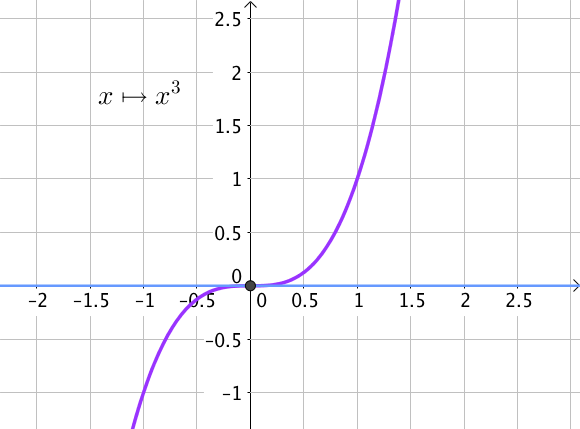
Parmi les fonctions usuelles, une fonction possède un point d’inflexion et constitue un exemple classique : c’est la fonction cube.
O l’origine du repère est un point d’inflexion.
En effet, pour $x \in \mathbb{R}, f'(x) = 3x^2$ donc $f'(0) = 0$.
De plus, la courbe traverse la tangente en ce point donc O est bien un point d’inflexion.
Outil pour trouver un point d’inflexion
Outil pour trouver un point d’inflexion
I. Théorème
Quel est le théorème pour trouver un point d’inflexion ?
Soit $f$ une fonction définie sur $]a; b[$ telle que $f”$ existe sur $]a; b[$ et $x_0$ un point de l’intervalle $]a; b[$,
si $f”$ s’annule en $x_0$, en changeant de signe alors le point $M_0(x_0, f(x_0))$ est un point d’inflexion.
II. Exemple
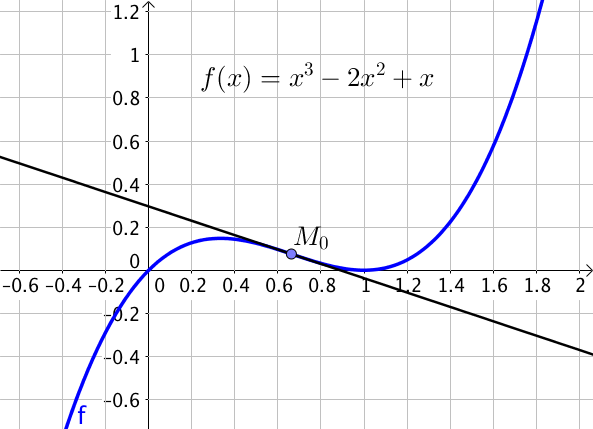
Soit $f$ la fonction définie par
$f(x) = x^3 – 2x^2 + x$ pour tout réel $x$,
on cherche d’éventuels points d’inflexion.
Pour cela, on calcule tout d’abord $f’$ qui existe car $f$ est polynomiale.
Pour tout $x \in \mathbb{R}, \ f'(x) = 3x^2 – 4x + 1$.
De même, $f’$ est dérivable sur $\mathbb{R}$ car c’est une fonction polynomiale : $f”$ existe donc et
$f”(x) = 6x – 4$.
Pour trouver un point d’inflexion, on cherche à présent une valeur de $x$ pour laquelle la dérivée seconde s’annule et change de signe.
Soit $x \in \mathbb{R}, \ f”(x) = 0 \iff 6x – 4 = 0 \iff x = \dfrac{4}{6} \iff x = \dfrac{2}{3}$.
La dérivée s’annule donc en $x = \dfrac{2}{3}$.
On dresse alors le tableau de signe de $f”(x)$ pour tout réel $x$.
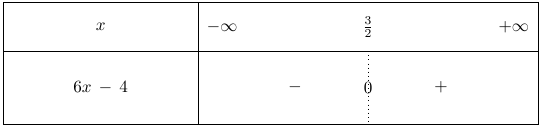
Ainsi, la dérivée seconde s’annule et change de signe en $x = \dfrac{2}{3}$.
Ainsi, $f$ admet un point d’inflexion en $x = \dfrac{2}{3}$.