Définition du logarithme népérien
Définition du logarithme népérien
Définition
La fonction logarithme népérien est l’unique fonction $f$, définie et dérivable sur $]0; +\infty[$ qui vérifie $\begin{array}{l} f(1) = 0 \\ f'(x) = \dfrac{1}{x} \end{array}$
On remarquera ici que l’on définit la fonction $f$ à partir de sa dérivée.
En outre, on peut noter que l’on ne connaissait jusqu’à présent pas de fonction dont la dérivée valait $\dfrac{1}{x}$.
En supposant que le cours portant sur les intégrales a déjà été étudié, on peut alors définir la fonction logarithme népérien, que l’on note $\ln$ comme étant la primitive de $x \mapsto \dfrac{1}{x}$ sur $]0; +\infty[$ et qui s’annule en $1$.
Ainsi, pour tout réel $x > 0$,
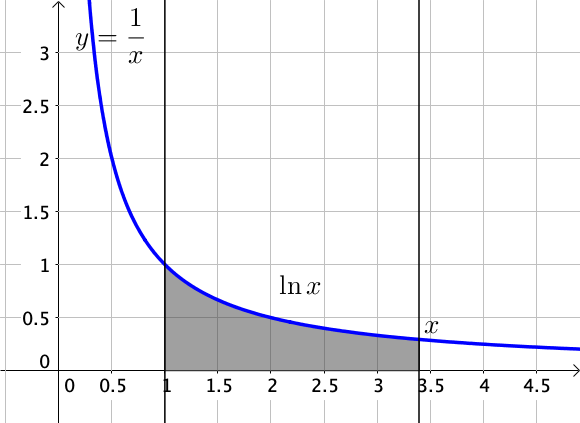
$\ln x = \displaystyle \int_1^x \dfrac{1}{t} dt$
On notera que lorsque $x = 1$, $\ln 1 = \displaystyle \int_1^1 \dfrac{1}{t} dt = 0$.
Graphiquement, la fonction $\ln x$ correspond à l’aire sous la courbe de la fonction inverse, comprise entre les droites verticales d’abscisse $1$ et $x$.
Propriétés analytiques
Propriétés analytiques
La fonction $\ln $ est définie et dérivable sur $]0;+\infty[$.
Pour tout réel $\displaystyle x>0, (\ln x)’= \dfrac{1}{x}$.
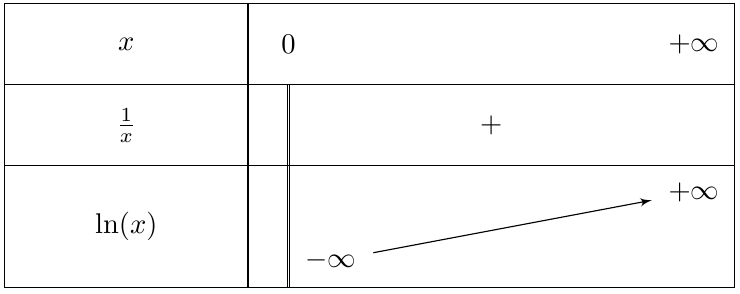
La fonction $\ln $ est continue et strictement croissante sur $]0;+\infty[$.
D’autre part,
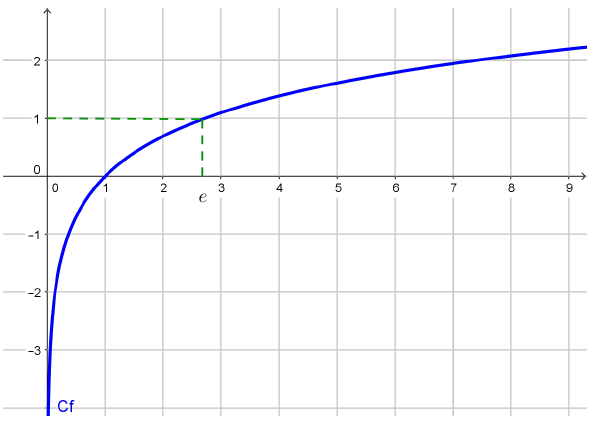
$\ln (1)=0$
$\ln (e)=1$
$\displaystyle\lim\limits_{x \rightarrow +\infty} \ln x= +\infty$
$\displaystyle \lim_{\substack{x \to 0\\ x > 0}} \ln x=-\infty$
Variations et représentation graphique
Théorème des croissances comparées
Théoréme des croissances comparées
Pour $n$ appartenant à $\mathbb{N}$ :
1. $\displaystyle \lim \limits_{\substack{x \to 0\\ x > 0}} x \ln x = 0$ et $\displaystyle \lim \limits_{\substack{x \to 0\\ x > 0}} x^n \ln x = 0.$
2. $\displaystyle \lim \limits_{x \rightarrow +\infty} \dfrac{\ln x}{x}=0$ et $\displaystyle \lim \limits_{x \rightarrow +\infty} \dfrac{\ln x}{x^n}=0.$
Exemple
Calculer $\displaystyle \lim \limits_{x \rightarrow +\infty} x^3-\ln x$.
étape 1 : On repére une forme indéterminée du type $\infty-\infty$ et on factorise par $x^3$.
$\displaystyle \lim \limits_{x \rightarrow +\infty} x^3-\ln x=\displaystyle \lim \limits_{x \rightarrow +\infty} x^3( 1- \dfrac{\ln x}{x^3}) $
étape 2 : On utilise le théoréme des croissances comparées pour lever l’indétermination.
On sait que: $\displaystyle \lim \limits_{x \rightarrow +\infty} \dfrac{\ln x}{x^3}= 0$.
Ainsi, le terme dans la parenthése tend vers $1$ et par produit de limites, on obtient :
$\displaystyle \lim \limits_{x \rightarrow +\infty} x^3( 1- \dfrac{\ln x}{x^3})=+\infty$
Nombre dérivé en 1
A savoir : $\displaystyle\lim_{h\to 0} \dfrac { \ln (1+h)}{h}=1$
Preuve :
On calcule $\displaystyle\lim_{h\to 0} \dfrac { \ln (1+h)}{h}$.
étape 1 : On réécrit la limite de manière à faire apparaître $\ln 1$ au numérateur et 1 au dénominateur.
On vérifie aisément que $h=1+h-1$.
$\displaystyle\lim_{h\to 0} \dfrac { \ln (1+h)}{h}=\displaystyle\lim_{h\to 0} \dfrac { \ln (1+h)-\ln 1}{1+h-1}$
étape 2 : On reconnaît la formule du nombre dérivé de la fonction $\ln $ en 1.
La fonction $\ln $ a pour dérivée la fonction $\displaystyle \dfrac{1}{x}$ qui prend donc la valeur 1 lorsque $x=1$.
Conclusion : $\displaystyle\lim_{h\to 0} \dfrac { \ln (1+h)-\ln 1}{(1+h)-1}=\displaystyle\lim_{h\to 0} \dfrac { \ln (1+h)}{h}=1.$
Propriétés algébriques
La fonction logarithme népérien
Définition
La fonction logarithme népérien est la fonction \(f\) définie et dérivable sur \(]0;+\infty[\) tel que
\(f(1)=0\) et \(f'(x)=\dfrac{1}{x}\)
\(\ln\) est la primitive de \(x\mapsto\dfrac{1}{x}\) sur \(]0;+\infty[\) qui s’annule en 1.
Propriétés algébriques
Pour tous réels $x>0$ et $y>0$ :
$\ln (xy)= \ln x+\ln y$
$\displaystyle \ln ( \displaystyle\frac{1}{x}) = -\ln x$
$\displaystyle \ln ( \displaystyle\frac{x}{y}) = \ln x-\ln y$
$\displaystyle \ln ( x^n) = n \ln x$ avec n $\epsilon$ $\mathbb{Z}$
Exemple :
Réduire : $A=\ln8-3\ln16$ et $B$= $\displaystyle \frac{4\ln9+5\ln27}{\ln3}$.
étape 1: On réécrit l’expression $A$ pour faire apparaître $\ln 2$.
$A=\ln 2^3-3\ln 2^4$
étape 2 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
$\displaystyle \ln (x^n)=n\ln x$ avec $\displaystyle n \in \mathbb{Z}$.
$A=3\ln 2-12\ln 2$
$A=-9\ln 2$
étape 3: On réécrit l’expression $B$ pour faire apparaître $\ln 3$.
$B$= $\displaystyle \frac{4\ln 3^2+5\ln 3^3}{\ln 3}$
étape 4 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
$\displaystyle \ln (x^n)=n\ln x$ avec $\displaystyle n \in \mathbb{Z}$.
$B$= $\displaystyle \frac{8\ln 3+15\ln 3}{\ln 3}$
On factorise par $\ln 3$ pour finir le calcul.
$B$= $\displaystyle \frac{23\ln 3}{\ln 3}$
$B$= 23
Autre exemple :
Simplifier : $C$= $\displaystyle \ln (x+3)+\ln 2-2\ln (x+1)$ en précisant l’intervalle d’étude.
étape 1 : On précise l’ensemble de définition de l’expression.
$x$ doit vérifier $x+3>0$ et $x+1>0$, c’est-à-dire :
$x>-3$ et $x>-1$.
La condition finale est donc: $x>-1$.
étape 2 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
- $ \ln (xy)=\ln x+\ln y$,
- $\ln (\displaystyle\frac{x}{y})=\ln x-\ln y$
- $\ln (x^n)=n\ln x$ avec $n \in \mathbb{Z}$
Ainsi,
$C$= $\displaystyle \ln (2x+6)-\ln (x+1)^2$
$C$= $\displaystyle \ln {\frac{2x+6}{(x+1)^2}}$
Équations, inéquations et logarithme népérien
Résolutions d’équations et inéquations avec la fonction $\ln$
Liens avec la fonction exponentielle :
Pour tout réel $x$, $\ln (e^x)=x$.
Pour tout réel $x>0$, $e^{\ln x}=x$.
Equations
Pour tous réels $x>0$ et $y>0$,
$\displaystyle \ln x=\ln y \iff x=y$.
Pour tout réel $x>0$ et tout réel $a$,
$\displaystyle \ln x=a\iff x=e^a$.
Inéquations
Pour tous réels $x>0$ et $y>0$,
$\displaystyle \ln x<\ln y \iff x < y$.
Pour tout réel $x>0$ et tout réel $a$,
$\displaystyle \ln x<a\iff x<e^a$.
Exemple
Résoudre $\displaystyle 3\ln (x+1)-3=0$ en précisant l’ensemble d’étude.
étape 1 :
On n’oublie pas de préciser l’ensemble de définition sur lequel on travaille.
$x$ doit vérifier : $x+1>0$ soit : $x>-1$.
On cherche donc des solutions sur $]-1;+\infty[$.
étape 2 :
On se ramène à une écriture du type : $\ln x=\ln y$ en utilisant $\ln e=1$.
$\displaystyle 3\ln (x+1)=3$
$\displaystyle \ln (x+1)=1$
$\displaystyle \ln (x+1)= \ln e$
étape 3 :
On sait que $\displaystyle \ln x=\ln y \iff x=y$ Ainsi :
$\displaystyle x+1= e$
$\displaystyle x= e-1$
étape 4 :
On conclut en donnant l’ensemble des solutions.
$\mathcal{S} = \{ e-1\}$
Autre exemple
Résoudre sur $]-1;+\infty[$ :
$\displaystyle \ln (x+3)-2\ln (x+1) \leqslant 0 $
étape 1 :
On sait que $\displaystyle \ln x \leqslant \ln y \iff x \leqslant y$ donc on réécrit l’expression pour faire apparaître l’inéquation entre deux logarithmes.
$\displaystyle \ln (x+3) \leqslant 2\ln (x+1)$ soit
$\displaystyle \ln (x+3) \leqslant \ln (x+1)^2$
étape 2 :
On applique les propriétés du logarithme sur les inéquations.
$\displaystyle \ln (x+3) \leqslant \ln (x+1)^2 \iff (x+3) \leqslant (x+1)^2$
$\displaystyle x+3 \leqslant x^2 + 2x +1$
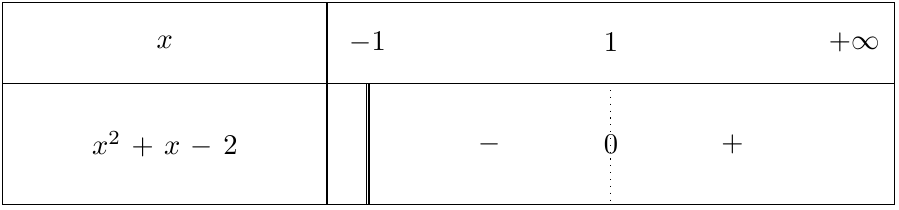
$\displaystyle x^2 + x -2 \geqslant 0$
étape 3 :
On remarque que $1$ est une solution évidente du trinôme où on calcule son discriminant et on trouve que $1$ et $-2$ sont les racines de $x^2 + x -2.$
étape 4 :
Pour déterminer le signe du trinôme, on utilise un tableau de signes uniquement sur l’ensemble de définition.
La racine $x=-2$ n’apparait donc pas :
étape 5 :
On fait attention à l’ensemble de définition de départ avant de conclure.
$\mathcal{S} = [1; +\infty[$
Fonctions composées - ln (u(x))
Fonctions composées $\ln(u(x))$
Théorème
Soit la fonction $f$ définie sur l’intervalle $I$ par:
$\displaystyle f(x) = \ln(u(x))$ où $u$ est une fonction dérivable et strictement positive sur $I$,
alors $f$ est dérivable sur $I$ et $f'(x) = \displaystyle\dfrac{u'(x)}{u(x)}.$
Exemple
Déterminer l’ensemble de définition et la dérivée de la fonction $f$ définie par :
$\displaystyle f(x) = \ln(x^2+x+1)$
Le discriminant $\Delta = 1-4= -3$ donc
$x^2+x+1 > 0$.
La fonction est donc définie et dérivable sur $\mathbb{R}$.
Pour tout $x \in \mathbb{R}$, on a :
$u(x)=x^2+x+1$ et $u'(x)=2x+1.$
Alors : $f'(x) = \displaystyle\frac{2x+1}{x^2+x+1}$.
Pour étudier les variations de cette fonction, on pourra juste étudier le signe de $2x+1$