Interférences
On étudie le phénomène des interférences et on essaie de définir ce que sont les interférences de la lumière.
Les interférences peuvent être de plusieurs types d’ondes. Une onde est la propagation d’une perturbation et ici, on se limite au cas de la lumière.
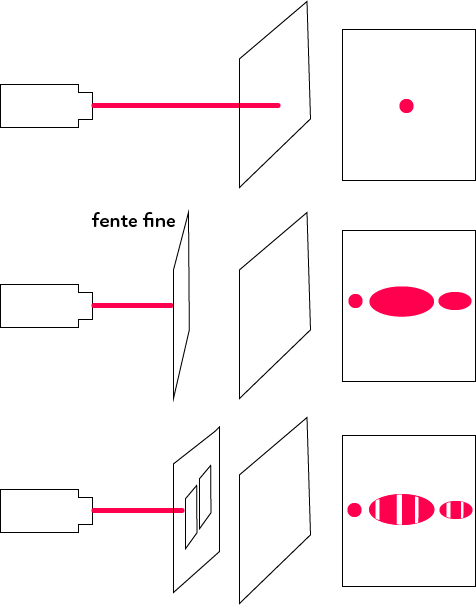
Exemple avec un faisceau laser
On a une source laser notée $S$ qui envoie un faisceau sur un écran. Lorsqu’on observe l’écran et qu’il n’y a rien entre le trajet de la source laser et de l’écran, on observe un point. Maintenant, si on met une fente fine ou un obstacle (un cheveu ou quelque chose qui gêne la propagation de cette lumière) avec un écran derrière, on observe une figure de diffraction. On a une tache centrale de diffraction et de part et d’autre des taches secondaires.
Avec toujours une même source laser, au lieu de mettre une fente fine, on place deux fentes fines qui sont parallèles et côte à côte. Elles sont vraiment fines par rapport à une grosse ouverture. Si la lumière rentre et qu’elle n’a pas changé de direction, cela donnerait juste un point. On observe, sur l’écran, la même figure globale à part que l’on voit des alternances de zones sombres et brillantes. On appelle cela des franges d’interférences. Cela s’appelle le phénomène d’interférence et la figure est une figure de diffraction et d’interférence.
Parfois on peut les confondre, mais on parle bien de franges d’interférence et de taches de diffraction. La dénomination est un peu différente.
Ensuite, pour essayer de comprendre ce qui s’est passé sur le trajet du faisceau laser obtenu par la source, on fait un petit schéma.
On a une source laser notée $S$ et, sur le trajet, on a ces deux fentes. Si elles sont vraiment très fines, elle se comportent comme de nouvelles sources car elles vont envoyer la lumière dans d’autres directions.
On trace un axe pour se repérer. Et on place deux nouvelles sources qui envoient la lumière dans d’autres directions. Si on regarde sur l’écran ce qu’il s’est passé, on va tracer le trajet de la lumière qui passe par la source $S_1$ et l’autre trajet qui passe par la source $S_2,$ qui représente les deux fentes. On observe un point $M.$
Que se passe-t-il et comment va-t-on interpréter ces franges sombres et brillantes ?
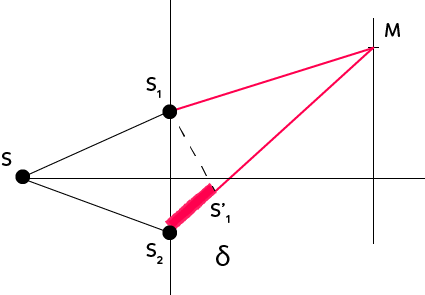
On a un trajet qui passe par $S,$ $S_1$ et $M,$ et un autre trajet qui passe par $S,$ $S_2$ et $M,$ également mais qui est plus long. On représente un plan passant par $S_1$ et $S_2$ pour dire qu’elles se situent sur un même plan. Le parcours de la lumière qui passe par $S_1M$ et différent de celui qui passe par $S_2M$.
Si on fait une projection ici, on construit le point $S’_1$ tel que $MS_1 = MS’_1$ par simple rotation ou par une projection non orthogonale. La différence de trajet qui est le trajet $S_2S’_1$ s’appelle la différence de marche. On l’appele $δ.$
Si $ δ = k\times λ$, sachant que la source laser a une fréquence et une longueur d’onde qui est la même que la lumière qui passe par les sources secondaires, on a des interférences constructives. Elles correspondent aux zones brillantes (les zones représentées en rouge).
Si par contre $ δ = (k+\dfrac{1}{2})\times λ$, on est dans le cas d’interférences destructives. Elles correspondent aux zones d’intensité minimale, les zones sombres.
Ces deux types d’interférences sont liées à la différence de marche qui existe sur le trajet de la lumière qui arrive à des endroits différents.
Diffraction
La diffraction est une propriété générale des ondes que l’on observe lorsqu’une onde rencontre un obstacle de petite dimension.
Exemple de la lumière
On étudie l’influence d’un obstacle sur la propagation d’un faisceau laser.
Cette expérience est reprise assez régulièrement en exercice et est aussi effectuée dans l’Épreuve des Capacités Expérimentales (ECE).
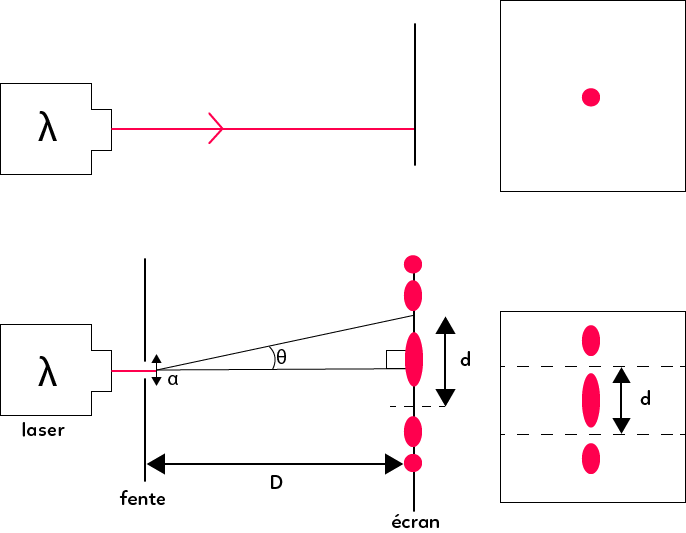
On a un faisceau laser de longueur d’onde $λ$ qui est envoyé sur un écran, on observe un point lumineux. Si on place sur le trajet du faisceau laser un obstacle de dimension $a$ (ici l’obstacle est une fente horizontale placée sur le trajet de la lumière), on observe un éparpillement de la lumière.
On observe donc une tache centrale très brillante et des taches secondaires de part et d’autre situées symétriquement par rapport à la tache centrale. Entre les taches centrales, on a des zones sombres qu’on appelle zones d’extinction. On caractérise le phénomène de diffraction par une grandeur qui s’appelle l’écart angulaire et qui est l’angle formé entre l’axe optique, qui passe par le centre de la fente et le centre de la tache centrale, et l’axe qui passe par le centre de la fente et le centre de la première zone d’extinction.
L’écart angulaire vérifie la relation : $Θ = \dfrac{λ}{a}$. $λ$ doit être exprimé en mètres (m), $a$ est exprimé en mètres également et $Θ$ est exprimé en radians (rad).
On peut aussi caractériser le phénomène de diffraction par la largeur de la tache centrale, qui se situe ici, entre les deux centres des zones d’extinction.
On va voir comment exprimer la largeur de la tache centrale en fonction des autres paramètres de l’expérience, c’est-à-dire : la longueur d’onde du laser, la dimension de l’obstacle, ici la fente, et la distance $D$ entre la fente et l’écran. Pour avoir cette relation, on exprime la tangente de $Θ$ dans le triangle rectangle ainsi constitué, qui est rectangle du côté de $d$ :
$tan Θ = \dfrac{\dfrac{d}{2}}{D}=\dfrac{d}{2D}$.
Il faut faire attention car on a seulement la moitié de la tache centrale, d’où $\dfrac{d}{2}$.
Ensuite, on fait l’approximation des petits angles qu’on utilise souvent en optique. Cette approximation consiste à dire que : $tan Θ \approx Θ$ lorsque les angles sont faibles. Avec cette approximation on peut donc dire que $ Θ = \dfrac{λ}{a} \approx \dfrac{d}{2D}$.
On a alors $d = \dfrac{2Dλ}{a}$. Ce qui correspond à la distance de la tache centrale. On remarque que si $D$ et $λ$ sont fixés (si on travaille toujours avec le même laser et si on maintient fixe la distance entre la fente et l’écran) si $a$ diminue (obstacle de plus petite dimension), $d$ augmente. Cela veut dire que plus l’obstacle est de petite taille, plus la figure de diffraction s’étend puisqu’on a une longueur de la tache centrale plus grande.
Si on se place dans le cas où $a$ et $D$ sont fixés (donc que la dimension de l’obstacle est fixe et la distance entre la fente et l’écran aussi) si $λ$ diminue (on change de laser et on en prend un bleu), la longueur de la tache centrale $d$ diminue.
Une conséquence de cette remarque est qu’avec une lumière polychromatique (qui a plusieurs radiations de plusieurs longueurs d’ondes) les figures de diffraction ne sont pas les mêmes. On a une superposition de toutes les figures de diffraction correspondantes aux radiations lumineuses qui constituent la lumière et on a une décomposition de la lumière.
On peut utiliser ce phénomène de diffraction pour déterminer la dimension de l’obstacle $a.$ Par exemple déterminer l’épaisseur d’un cheveu, qui conduit à ce phénomène de diffraction. Pour cela, il suffit d’utiliser la formule, mais de l’exprimer de la manière suivante : $a = \dfrac{2Dλ}{d}$ et qui est aussi exprimée en mètres (m).