Effet Doppler - Applications à l'astrophysique
Effet Doppler : applications à l’astrophysique
Une application de l’effet Doppler est l’effet Doppler-Fizeau. L’effet Doppler s’applique à la lumière qui est une onde électromagnétique et permet de quantifier l’éloignement ou le rapprochement d’une étoile.
Si une étoile s’éloigne de la Terre, on observe un décalage du spectre de sa lumière vers les basses fréquences (c’est à dire vers les hautes longueurs d’ondes), ce qui équivaut à un décalage vers le domaine du rouge.
Si une étoile se rapproche de la Terre, on observe un décalage du spectre de sa lumière vers les hautes fréquences (c’est à dire vers les basses longueurs d’onde), ce qui revient à un décalage vers le domaine du bleu.
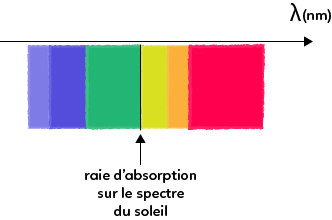
On mesure ce décalage en se basant sur les raies d’absorption d’une espèce chimique connue et en comparant la position de celles-ci sur le spectre du Soleil, étoile considérée comme fixe par rapport à la Terre, et sur le spectre de l’étoile.
Si le décalage se fait vers le rouge, l’étoile s’éloigne. Si le décalage se fait vers le bleu, l’étoile se rapproche.
D’une manière générale, on constate que les raies se décalent vers le domaine du rouge, constituant un argument un faveur de l’expansion de l’Univers.
Effet Doppler - Les formules
Effet Doppler : les formules
L’effet Doppler est une propriété générale des ondes qui s’observe pour les ondes mécaniques ou sonores et les ondes électromagnétiques comme la lumière. Il se manifeste lorsque l’émetteur de l’onde est en mouvement par rapport à un récepteur. Il existe différentes configurations possibles, selon le mouvement du récepteur et de l’émetteur.
Dans ce qui suit, on se limite au cas où le récepteur est fixe et l’émetteur en mouvement.
On considère un émetteur d’onde de fréquence $f_e$ et de célérité $c$ qui est en mouvement par rapport à un récepteur fixe, à une vitesse $v$.
On suppose dans un premier temps que l’émetteur s’approche du récepteur et on constate alors que la fréquence reçue par le récepteur $f_r$ est différente de la fréquence émise $f_e$ et vaut :
$f_r = f_e \times \dfrac{c}{c – v} $
Les deux fréquences doivent être exprimées en Hz alors que la vitesse et la célérité sont exprimées en $\text{m.s}^{-1}$.
Puisque la vitesse $v$ est par définition positive, on peut écrire :
$ -v < 0 \iff c – v < c \iff 1 < \dfrac{c}{c – v} \iff f_e < f_e \times \dfrac{c}{c – v} \iff f_e < f_r $
On s’intéresse désormais au cas où l’émetteur s’éloigne du récepteur et on peut écrire la relation suivante :
$f_r = f_e \times \dfrac{c}{c + v}$
La vitesse étant toujours positive, on peut écrire :
$ v > 0 \iff c + v > c \iff 1 > \dfrac{c}{c + v} \iff f_e > f_e \times \dfrac{c}{c + v} \iff f_e > f_r$
L’effet Doppler est appréciable au quotidien. Il s’agit par exemple de la variation sonore que l’on entend lors du passage d’une ambulance. Lorsque l’ambulance s’approche, on entend un son plus aigu : la fréquence reçue est supérieure à la fréquence émise. Lorsque l’ambulance s’éloigne, on entend un son plus grave : la fréquence reçue est inférieure à la fréquence émise.
Il est également utilisé pour mesurer des vitesses, lors de contrôles autoroutiers avec les radars.
En effet, en considérant une voiture qui s’approche du récepteur, on dispose de la formule suivante : $f_r = f_e \times \dfrac{c}{c – v} $
Que l’on peut réécrire sous la forme : $f_r \times c – f_r \times v =f_e \times c $
Ce qui permet d’obtenir : $ v = \dfrac{(f_r – f_e) c }{f_r}$
En connaissant la fréquence des ondes émise et reçue ainsi que leur célérité, on peut en déduire la vitesse $v$ de l’émetteur par rapport au récepteur.


