Le grossissement
I. La lunette astronomique
La lunette astronomique est un système afocal : c’est-à-dire que si on prend un objet à l’infini, il le transforme en une image à l’infini.
Le rayon qui provient de cet objet à l’infini n’est pas dévié :
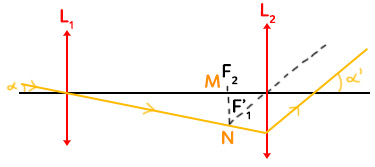
Ce qu’il faut retenir c’est que si un rayon est entré par rapport un angle $\alpha$ à l’axe optique, il ressort avec un angle $\alpha ’$. $\alpha ’$ qui est plus grand que $\alpha $ parce que, dans une lunette astronomique, la distance focale de la lentille L1 est plus grande que celle de la lentille L2.
F’1 et f2 sont confondus : c’est ça le principe d’un système afocal.
II. Le grossissement
Le grossissement est égal à : $\dfrac{\alpha ’}{\alpha}$.
Cette équivalence n’est pas propre à la lunette astronomique, elle est générale et s’applique à tout système.
On va tout d’abord faire l’hypothèse des petits angles : $\alpha$ et $\alpha ’$ sont très petits devant 1. Attention, l’unité standard pour les angles en maths et physique est le radian et non le degré !
On calcule ce que vaut $tan{\alpha}$ : $tan{\alpha} = \dfrac{MN}{f’1}$.
Grâce à l’hypothèse des petits angles, on peut dire que $tan{\alpha} \approx \alpha$.
Prenons $tan{\alpha’}$ : $tan{\alpha’} = \dfrac{MN}{f’2}$.
Puisque l’on est toujours dans l’hypothèse des petits angles, $tan{\alpha’} \approx \alpha’$.
Donc le grossissement vaut : $G = \dfrac{\alpha ’}{\alpha} = \dfrac{MN}{f’2}\times \dfrac{f’1}{MN} = \dfrac{f’1}{f’2}$.
En raisonnant avec les grandeurs algébriques, on serait plus précis et on verrait que le grossissement est négatif.
Ici, la notion n’est pas algébrique. Attention, f’1 et f’2 doivent avoir la même unité. Par exemple, si f’1 = 1m et f’2 = 10 mm. On aura $G = \dfrac{1}{10.10^{-3}} = 100.$ Sans unités !
La lunette astronomique
I. Notion d’infini en optique
L’infini est très loin comparé aux dimensions du système optique. Les dimensions du système optique peuvent être les dimensions de la lentille, mais aussi ses caractéristiques (distance focale, etc). Si l’objet ou l’image est très éloigné de cette valeur, on considère qu’il est à l’infini.
On modélise l’objet ou l’image à l’infini par des rayons parallèles entre-eux. Si c’est un objet à l’infini, il émet des rayons parallèles entre-eux. Si des rayons parallèles entre-eux sortent, c’est que l’image est à l’infini.
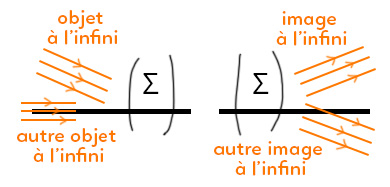
Le fait que les rayons représentés sur le schéma de gauche ne soient pas tous parallèles entre-eux symbolise qu’il y a deux objets. De même pour les images sur le schéma de droite.
II. Principe de la lunette astronomique
C’est un ensemble de deux lentilles convergentes L1 et L2 qui ont aussi un nom : objectif (L1) et oculaire (L2).
Le principe est que le point focal image de la première lentille est confondu avec le point focal objet de la deuxième lentille. F’1 (point focal image L1) est confondu avec F2 (point focal objet L2).
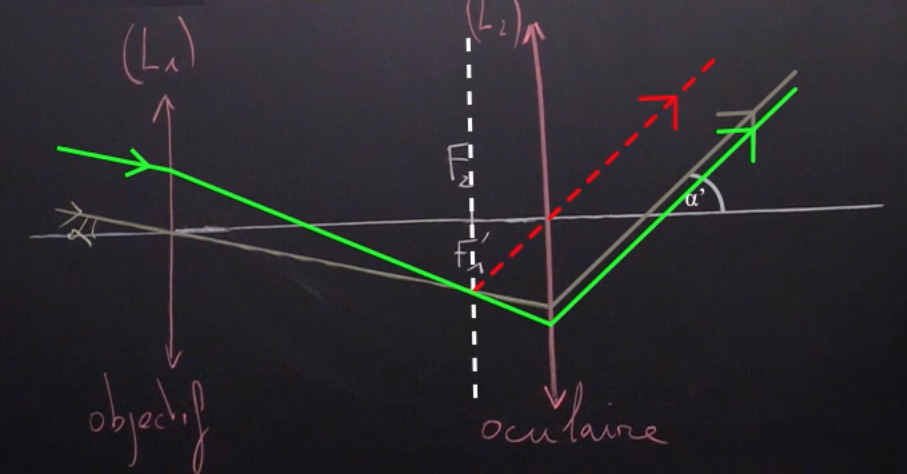
Un rayon lumineux arrive sur la lentille L1 avec un angle alpha. Le rayon lumineux choisi est un peu particulier puisqu’il passe par le centre optique de la première lentille, donc il n’est pas dévié. Il arrive sur la deuxième lentille (oculaire). Ensuite, on doit utiliser différentes règles de construction pour savoir comment le rayon va être dévié. Deux rayons incidents parallèles entre-eux se coupent après la lentille dans le plan focal image. Deux rayons issus d’un point, dans le plan focal objet d’une lentille, émergent de cette lentille, parallèles entre-eux. On peut donc construire la suite de ce rayon d’intérêt.
Les rayons de construction sont tracés en pointillés. Le rayon sort avec un angle alpha’ par rapport à l’axe optique. On remarque qu’il est plus grand que l’angle alpha de départ. Si on a un deuxième rayon parallèle au premier (en vert), on peut le tracer dans le plan de cette façon, selon les règles de construction. Ils sont rentrés parallèles entre-eux, ils ressortent parallèles entre-eux. C’est un système afocal. Un objet à l’infini génère une image, elle-aussi, à l’infini.
III. Pourquoi voit-on plus gros ?
Qu’est-ce qui change, pour un œil, de voir un rayon qui arrive avec un angle alpha par rapport à la direction observée vis-à-vis d’un rayon qui rentre avec un angle alpha’ ?
Pour rappel, la lentille est convergente. On retrouve l’axe optique avec les deux angles à comparer alpha et alpha’. Les rayons passent par le centre de l’axe optique du cristallin et ne sont pas déviés. Ils frappent ensuite la rétine. Si l’angle est plus petit, l’image formée sera plus petite. En fait, c’est plus gros car l’image prend plus de place sur la rétine.


