Division euclidienne
Division euclidienne
Définition
Un nombre entier est un nombre qui permet de compter un nombre d’entités par exemple (0; 1; 2, …).
On considère deux nombres entiers $n$ et $d (\neq 0)$.
La division euclidienne de $n$ par $d$ consiste à trouver deux nombres $q$ (le quotient) et $r$ (le reste) tels que $n = d \times q + r$ avec $r < d$.
Le nombre $n$ correspond au dividende, le nombre $d$ au diviseur.

Il s’agit en fait d’effectuer un partage équitable.
Par exemple, $n$ peut représenter le nombre de billes à répartir parmi $d$ élèves.
On souhaite que chacun en ait le même nombre $q$ et il restera des billes en une quantité $r$ qui ne seront pas distribuées.
On impose également que le partage soit généreux, cela signifie que le reste est toujours plus petit que le diviseur ou encore $r < d$.
En effet, si il restait plus de billes que d’élèves, on pourrait encore donner des billes aux élèves sans qu’aucun d’eux ne soit lésé.
Exemple :
On considère que $n = 17$ et $d= 5$.
On regarde la table de $5$ pour trouver le plus grand nombre $q$.
Ici, $q = 3$ ($5 \times 3 = 15$) car si on avait choisit $q = 4$, on aurait alors eu $4 \times 5 = 20 > 17 = n$ ce qui n’est pas possible.
Ainsi, $17 = 5 \times 3 + 2$.
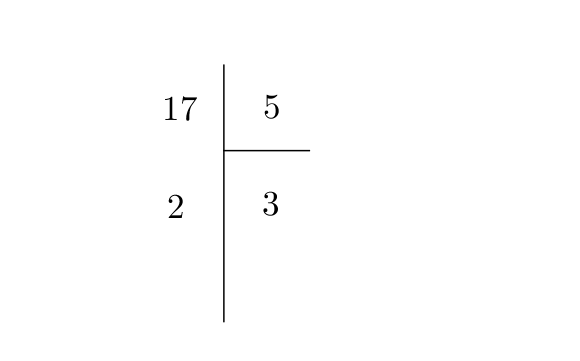
Nombres premiers
Nombres premiers
Définition
Un nombre est dit premier s’il est divisible seulement par $1$ et par lui même, c’est à dire si il admet deux diviseurs différents.
Remarque :
$0$ et $1$ ne sont pas des nombres premiers. En effet, $1$ admet un seul diviseur : lui même.
Exemples :
$2$ n’est divisible que par $1$ et $2$, c’est donc un nombre premier. C’est le seul nombre pair qui est premier.
En effet, si on considère le nombre $4$, ses diviseurs sont $1, 2, 4$ : il n’est donc pas premier.
Tous les nombres pairs différents de $2$ ne sont donc pas premiers, car étant divisible par deux ils admettent au moins trois diviseurs.
Propriété
Il existe une infinité de nombres premiers.
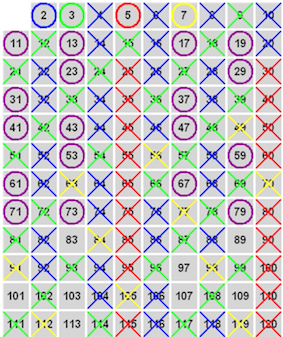
Le crible d’Eratosthène permet de trouver les nombres premiers.
Il consiste à considérer tous les nombres, jusqu’à 120 ici.
Le premier nombre est 2. C’est un nombre premier.
On raye ensuite tous les multiples de 2, qui sont donc divisibles par 2 et qui possèdent ainsi au moins 3 diviseurs différents.
On considère le nombre suivant qui n’est pas barré, c’est à dire $3$, puis on barre tous les multiples de 3, pour la même raison que précédemment.
On continue de même en prenant le nombre suivant qui n’est pas barré et en barrant les multiples de ce nombre.