Homothéties
Homothéties
Définition
Les homothéties sont des transformations du plan qui génèrent des agrandissements ou des réductions.
Une homothétie est définie par un centre $O$ et un rapport $k$.
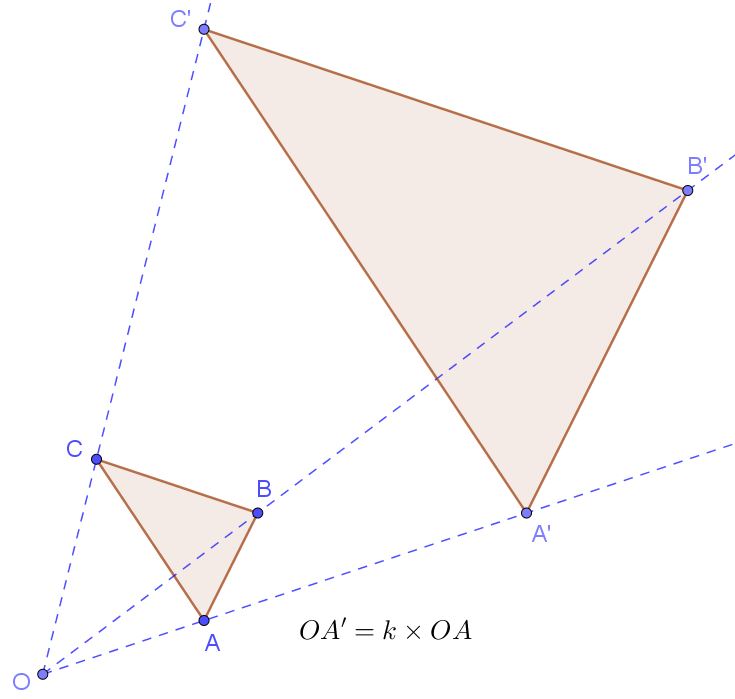
Sur la figure suivante, les points $O;A$ et $A’$ vériofient : $OA’=k\times OA$
Exemple :
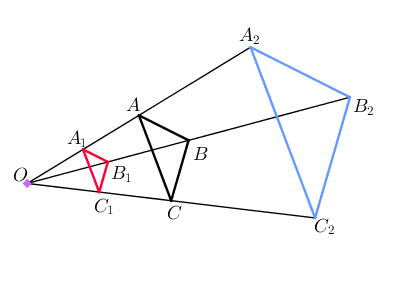
On considère un triangle $ABC$ représenté en noir et un point $O$.
Afin d’obtenir le triangle $A_2B_2C_2$ qui est le triangle obtenu par l’homothétie de centre $O$ et de rapport $k = 2$ du triangle $ABC$, il faut donc se servir de la relation : ${OA}_2 = 2 OA$
Cette homothétie génère donc un agrandissement, toutes les longueurs sont multipliées par 2.
Afin d’obtenir le triangle $A_1B_1C_1$ qui est le triangle obtenu par l’homothétie de centre $O$ et de rapport $k = 0,5$ du triangle $ABC$, il faut donc se servir de la relation : ${OA}_1 = 0,5 OA$
Cette homothétie génère donc une réduction, toutes les longueurs sont multipliées par 0,5.
A l’issue des deux homothéties, on obtient la figure suivante :
Propriétés
Une homothétie conserve les mesures d’angles.
Les longueurs sont multipliées par $k$.
Les aires sont multipliées par $k^2$.
Lorsque le rapport $k$ est négatif, la figure s’inverse. (non visible sur la figure)