Triangles égaux
Triangles égaux
Définition
Deux triangles sont égaux (ou superposables) si leurs côtés sont deux à deux de même longueur.
Exemple
Les triangles $IKS$ et $TOC$ sont égaux.
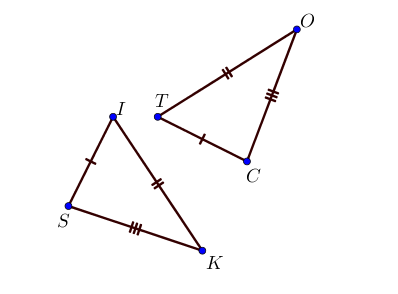
Ces deux triangles sont superposables car en les découpant, on peut les mettre l’un sur l’autre.
Propriété 1
Si deux triangles ont deux côtés de même longueur compris entre deux angles respectivement égaux alors ces triangles sont égaux.
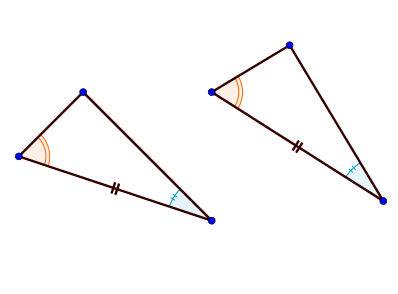
Propriété 2
Si deux triangles ont deux angles égaux formés par des côtés respectivement égaux alors ces triangles sont égaux.
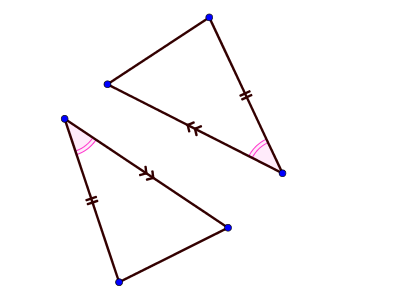
Triangles semblables
Triangles semblables
Définition
Deux triangles sont semblables lorsqu’ils ont les mêmes angles deux à deux.
Deux triangles peuvent être semblables sans avoir les mêmes longueurs.
Exemple :
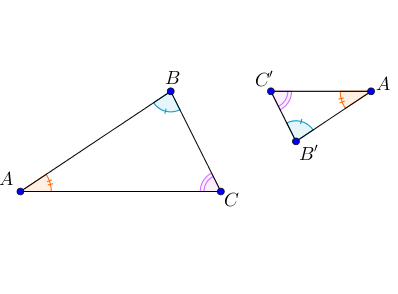
Les triangles $ABC$ et $A’B’C’$ sont semblables.
Propriété :
Si deux triangles ont leurs côtés respectivement proportionnels alors ils sont semblables.
Exemple :
Soient deux triangles $SKI$ et $TOC$.
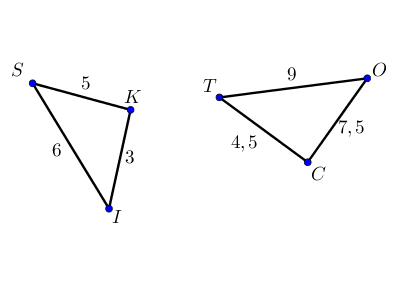
Considérons le rapport des longueurs.
On commence par calculer le rapport des longueurs les plus grandes dans le triangle :
$\dfrac{TO}{SI} = \dfrac{9}{6} = \dfrac{3}{2}$.
On calcule ensuite le rapport des longueurs “moyennes” :
$\dfrac{CO}{SK} = \dfrac{7,5}{5} = \dfrac{3}{2}$.
Enfin, on calcule le rapport des plus petites longueurs :
$\dfrac{TC}{IK} = \dfrac{4,5}{3} = \dfrac{3}{2}$.
Ainsi, les longueurs des triangles sont proportionnelles : les triangles sont donc semblables.
Leurs angles sont donc égaux deux à deux.


