Nombres complexes et vecteurs
Nombres complexes et vecteurs
Distances et vecteurs
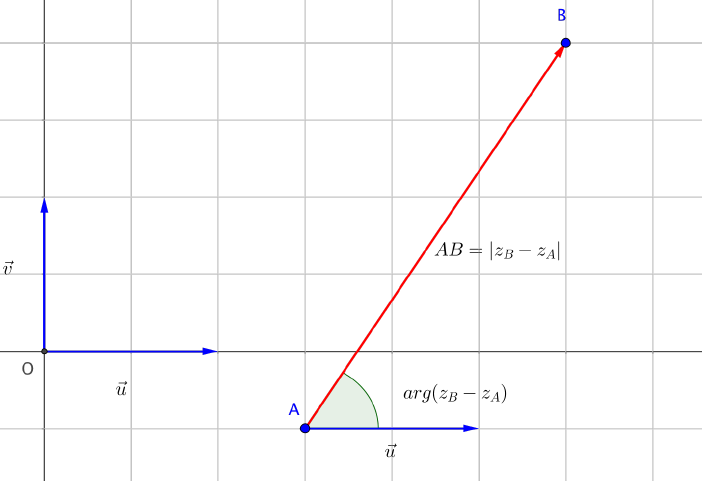
On considére deux points $A$($z_A$) et $B$($z_B$) du plan complexe $\left(O;\overrightarrow{u};\overrightarrow{v}\right)$.
Le milieu $I$ du segment $[AB]$ a pour affixe :
$z_I=\dfrac{z_A+z_B}{2}$.
Le vecteur $\overrightarrow{AB}$ a pour affixe $z_B-z_A$.
Il en résulte donc que la distance $AB$ vaut :
$AB=|z_B-z_A|$.
Angles et arguments
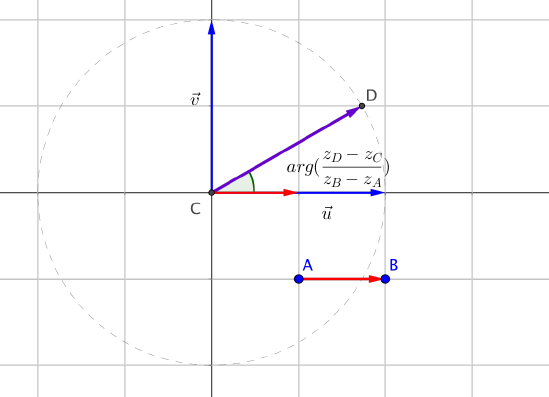
Soient $A(z_A)$, $B(z_B)$, $C(z_C)$ et $D(z_D)$ quatre points du plan complexe $\left(O;\overrightarrow{u};\overrightarrow{v}\right)$.
On a les résultats suivants :
$ \boxed{ arg(z_B-z_A)=(\overrightarrow{u},\overrightarrow{AB}) ~ [2\pi]}$
$\boxed{ arg\bigg(\dfrac{z_D-z_C}{z_B-z_A}\bigg) = (\overrightarrow{AB},\overrightarrow{CD}) ~ [2\pi]}$
Exemple
On donne les quatre points suivants :
$A(0,0)$, $B(\dfrac{\sqrt3}{2},\dfrac12)$, $C(\dfrac12,-\dfrac12)$ et $D(1,-\dfrac12)$.
Calculer une mesure de l’angle $(\overrightarrow{AB},\overrightarrow{CD})$.
On commence par donner l’affixe des quatre points :
- $ z_A=0$
- $z_B=\dfrac{\sqrt3}{2}+\dfrac12 i$
- $z_C=\dfrac12-\dfrac12 i$
- $z_D=1-\dfrac12 i$
On a alors :
$\dfrac{z_D-z_C}{z_B-z_A} = \dfrac{(1-\dfrac12 i)-(\dfrac12-\dfrac12 i)}{(\dfrac{\sqrt3}{2}+\dfrac12 i)-(0)} $
$\dfrac{z_D-z_C}{z_B-z_A} = \dfrac{\dfrac12}{\dfrac{\sqrt3}{2}+\dfrac12 i}$.
En simplifiant par $2$ puis en multipliant par la quantité conjuguée, on a :
$\dfrac{z_D-z_C}{z_B-z_A}=\dfrac{\sqrt3-i}{4} $
$\dfrac{z_D-z_C}{z_B-z_A} = \dfrac{1}{2}\times \left( \dfrac{\sqrt3}{2}-\dfrac12 i\right)$
En utilisant les méthodes précédentes, on montre facilement que :
$arg\left( \dfrac{\sqrt3}{2}-\dfrac12 i\right) = -\dfrac{\pi}{6} ~ [2\pi] $.
On trouve donc :
$arg\bigg(\dfrac{z_D-z_C}{z_B-z_A}\bigg) = -\dfrac{\pi}{6} ~ [2\pi] $.
Conclusion :
Comme
$arg\bigg(\dfrac{z_D-z_C}{z_B-z_A}\bigg) = (\overrightarrow{AB},\overrightarrow{CD}) ~ [2\pi]$,
on a donc :
$(\overrightarrow{AB},\overrightarrow{CD})=-\dfrac{\pi}{6} ~ [2\pi]$
Complexes et ensembles de points - Exercice 1
Exercice
Déterminons l’ensemble des points \(M(z)\) du plan vérifiant \(\left|z – 2i \right| = 3\).
Étape 1 : On pose le point \(A\) d’affixe \(2i\).
Étape 2 : On reconnait le module de l’affixe du vecteur \(\overrightarrow{AM}\) qui est aussi la longueur \(AM\).
Étape 3 : L’ensemble des points recherché se situe sur un cercle de centre \(A\) et de rayon 3.
Complexes et ensembles de points : exercice 2
Exercice
Déterminons l’ensemble des points \(M(z)\) du plan vérifiant \(\left|z + 3i + 1 \right| = \left|iz – 3i \right|\).
Étape 1 : On modifie l’expression de sorte à faire apparaître une forme du type \( \left|z_A – z_B\right|\).
Étape 2 : On pose le point \(B\) d’affixe \(-3i – 1\) tel que nous venons de le définir.
Étape 3 : On déduit de cette expression qu’il s’agit de la longueur \(MB\).
Étape 4 : On factorise la deuxième expression par \(i\).
Étape 5 : On sait que le module d’un produit est le produit des modules.
Étape 6 : On pose le point \(A\) d’affixe 3. Et on en déduit que l’expression correspond à la longueur \(MA\).
Étape 7 : L’ensemble des points se trouve donc sur la médiatrice de \([AB]\) que nous pouvons tracer.
Complexes et ensembles de points : Exercice 3
Exercice
Déterminons l’ensemble des points \(M(z)\) du plan vérifiant \(arg(z – 2i) = \frac{\pi}{3} [2\pi]\).
Étape 1 : On sait que \( arg(z_B – z_A) = (\overrightarrow{u} ; \overrightarrow{AB}) [2\pi]\).
Étape 2 : On pose le point \(C\) d’affixe \(2i\).
Étape 3 : On en déduit d’après le cours que l’angle formé entre les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{CM}\) vaut \(\frac{\pi}{3}\).
Étape 4 : On n’oublie pas qu’un angle de \(\frac{\pi}{3}\) est égal à \(60^o\) (soit \(\frac{180^o}{3}\)).
Étape 5 : On conclut en disant que l’ensemble des solutions est la demi droite \(Cx\) avec \(C\) exclu.
Caractérisation de nombres complexes
Caractérisations des nombres complexes
Réels et imaginaires purs
Soit $z=a+ib$ un nombre complexe quelconque.
On dit que $z$ est réel lorsque $b=0$ et que $z$ est imaginaire pur lorsque $a=0$.
Exemple
- $2i$ est imaginaire pur,
- $3$ est réel
- $3+2i$ n’est ni réel, ni imaginaire pur.
Caractérisation avec les parties réelles et imaginaires
On constate simplement que si $z$ est un nombre complexe non nul, $\boxed{z\in \mathbb{R} \Leftrightarrow Im(z)=0}$.
Autrement dit, $z$ est réel si et seulement si sa partie imaginaire est nulle.
De même, $z$ est imaginaire pur si et seulement si sa partie réelle est nulle : $\boxed{z\in i\mathbb{R} \Leftrightarrow Re(z)=0}$.
Caractérisation avec l’argument
Soit $z$ un nombre complexe non nul.
$\bullet$ $z$ est réel si et seulement si $arg(z)=k\pi$ avec $k\in \mathbb{Z}$.
$\bullet$ $z$ est imaginaire pur si et seulement si $arg(z)=\dfrac{\pi}{2}+k\pi$ avec $k\in \mathbb{Z}$.
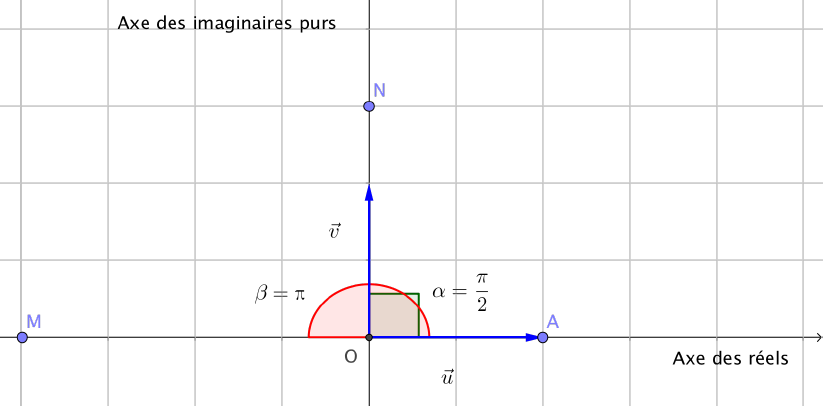
Illustration graphique
L’affixe du point $M$ est un réel négatif, tandis que l’affixe du point $N$ est imaginaire pur.
le point $A$ a un affixe réel égal à $1$.