Opérations sur les limites
Opérations sur les limites
Opérations sur les limites
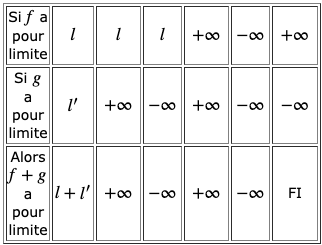
Limite d’une somme
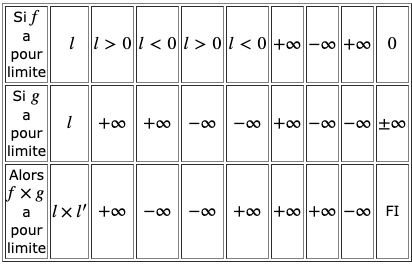
Limite d’un produit
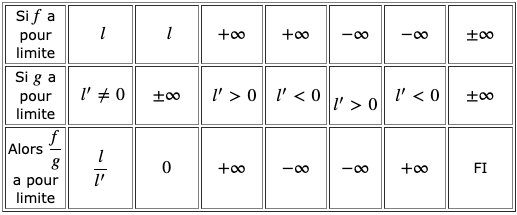
Limite d’un quotient dans le cas où la limite du dénominateur n’est pas nulle
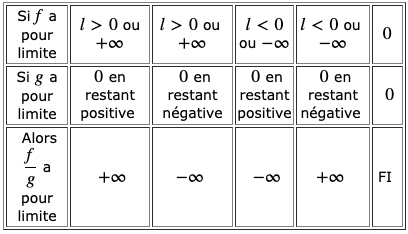
Limite d’un quotient dans le cas où la limite du dénominateur est nulle
Opérations sur les limites - Exercice 1
Opérations sur les limites - Exercice
Calculer \(\lim\limits_{\begin{array}{l}x \to 1\\x < 1\end{array}} \dfrac{2}{x^2 – 1}\).
Ce qu’il faut savoir faire :
- Étape 1: On étudie le signe du trinôme.
- Étape 2: On en déduit que le dénominateur tend vers \(0\) par valeurs négatives.
- Étape 3: On peut conclure que la fonction tend vers \(- \infty \).