Projection orthogonale
Projection orthogonale dans l’espace
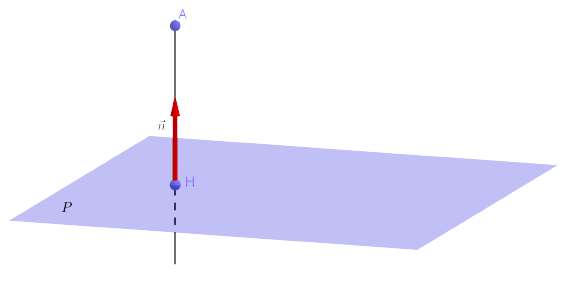
Sur un plan : définition
Le projeté d’un point \(A\) sur un plan est le point \(H\) du plan tel que \(\overrightarrow{AH}\) est orthogonal au plan.
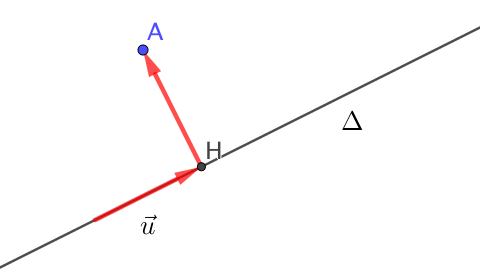
Sur une droite : définition
Le projeté orthogonal d’un point \(A\) sur une droite \(\Delta\) est le point \(H\) vérifiant :
\( \left\{ \begin{array}{ll} H \in \Delta \\ \overrightarrow{AH} . \overrightarrow{u} = 0 \end{array} \right. \)
où \(\overrightarrow{u}\) est un vecteur directeur de la droite \(\Delta\).
Projeté orthogonal d'un point (démonstration)
Orthogonalité
Orthogonalité
I) Orthogonalité de deux droites dans l’espace
Propriété :
Soient $(D)$ et $(D’)$ deux droites de vecteurs directeurs $\overrightarrow{d}$ et $\overrightarrow{d’}$,
$(D)$ est orthogonale à $(D’)$ si et seulement si :
$\overrightarrow{d}.\overrightarrow{d’}=0$
Remarque :
Dans l’espace, on utilise le terme orthogonal lorsque le produit scalaire de deux droites est nul.
Le terme perpendiculaire est utilisé lorsque deux droites sont orthogonales et sécantes, c’est à dire qu’elles sont orthogonales et coplanaires.
Exemple :
On considère deux droites $(D)$ et $(D’)$ de représentations paramétriques :
$(D)\left \{ \begin{array}{l} x = 1 – 3t \\ y = 2t \\ z = 4 – t \end{array} \right. (t \in \mathbb{R})$
et $(D’)\left \{ \begin{array}{l} x = t \\ y = 2+ 2t \\ z = -5t – 1 \end{array} \right. (t \in \mathbb{R})$
$(D)$ et $(D’)$ sont-elles orthogonales ?
La première étape consiste à déterminer les vecteurs directeurs des deux droites.
Pour rappel, il s’agit des coefficients multiplicateurs de la variable, (ici c’est le réel $t$).
Ainsi, $\overrightarrow{d} \left ( \begin{array}{c} -3 \\ 2 \\ -1 \end{array} \right )$ et $\overrightarrow{d’} \left ( \begin{array}{c} 1 \\ 2 \\ -5 \end{array} \right )$.
Il s’agit ensuite de calculer leur produit scalaire, qui vaut la somme des produits des coordonnées :
$\overrightarrow{d}.\overrightarrow{d’}= -3 + 4 + 5 = 6 \neq 0$.
Finalement, $(D)$ et $(D’)$ ne sont pas orthogonales.
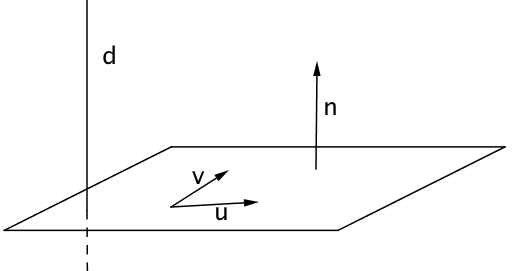
II) Orthogonalité d’une droite et d’un plan
Propriété :
Soit $(D)$ une droite de vecteur directeur $\overrightarrow{d}$ et $\mathcal{P}$ un plan dirigé par un couple de vecteur $(\overrightarrow{u}, \overrightarrow{v})$ non colinéaires et de vecteur normale $\overrightarrow{n}$.
$(D)$ est orthogonale à $\mathcal{P}$ si et seulement si :
- $\overrightarrow{d}.\overrightarrow{u} = 0$ ET
- $\overrightarrow{d}.\overrightarrow{v} = 0$, car lorsqu’une droite est orthogonale à deux droites d’un plan, elle est orthogonale à toute droite du plan
OU
- $\overrightarrow{d}$ et $\overrightarrow{n}$ sont colinéaires.
Exemple :
Soit $\mathcal{P}$ un plan d’équation cartésienne $2x -3y + 4z – 2 = 0$ et $(D)$ de représentation paramétrique
$(D)\left \{ \begin{array}{l} x = -2-4t \\ y = 12 + 6t \\ z = -8 t \end{array} \right. (t \in \mathbb{R})$
$(D)$ est-elle orthogonale au plan $\mathcal{P}$ ?
On peut aisément trouver le vecteur directeur de la droite et le vecteur normal du plan :
$\overrightarrow{d} \left ( \begin{array}{c} -4 \\ 6 \\ -8 \end{array} \right )$ et $\overrightarrow{n} \left ( \begin{array}{c} 2 \\ -3 \\ 4 \end{array} \right )$.
On peut alors remarquer que $\overrightarrow{d} = -2\overrightarrow{n}$, c’est à dire que $\overrightarrow{d}$ et $\overrightarrow{n}$ sont colinéaires.
Ainsi $(D)$ est orthogonale au plan $\mathcal{P}$.