Fonction de répartition
Fonction de répartition
Définition
Comment est définie la fonction de répartition d’une variable aléatoire ? Comment trouver une fonction de répartition ?
Soit $X$ une variable aléatoire qui suit une loi de densité $f$ sur $[a; b]$.
On appelle fonction de répartition de la variable $X$, la fonction $F$ définie sur $[a; b]$ par $F(x) = P(X \leq x)$.
Or comme $X$ prend ses valeurs sur l’intervalle $[a; b]$, on peut écrire aussi que : $F(x) = P(a < X \leq x)$.
Enfin, comme $X$ suit une loi de densité, la probabilité associée s’écrit à l’aide d’une intégrale.
Donc $F(x) = \displaystyle \int_a^x f(t) \,dt$
On prêtera une attention particulière à ne pas utiliser la même variable à la borne de l’intégrale $x$ pour la variable d’intégration ($t$ ici).
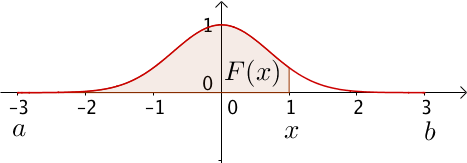
Graphiquement, $F(x)$ est l’aire entre la courbe de $f$, l’axe des abscisses et les droites verticales en $a$ et $x$.
Exercice :
Soit $X$ une variable aléatoire de fonction de densité $f(x) = \dfrac{1}{2} x$ sur $[0; 2]$.
Déterminer $F(x)$.
Soit $x \in [0; 2]$,
$F(x) = \displaystyle \int_0^x \dfrac{1}{2}t \, dt$.
On cherche donc une primitive de $\dfrac{1}{2}t$.
$\displaystyle \int_0^x \dfrac{1}{2}t \, dt = \left [ \dfrac{t^2}{4} \right ]_0^x = \dfrac{x^2}{4} – \dfrac{0^2}{4}$
Finalement, $F(x) = \dfrac{x^2}{4}$