Limites de suites
Limites de suites
Définitions :
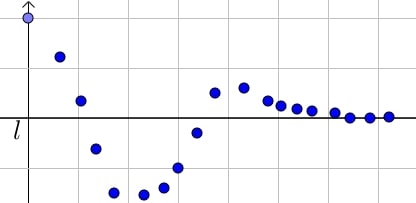
On dit que $(u_n)$ admet pour limite $l$ si pour $n$ suffisamment grand, les termes de la suite $(u_n)$ se rapprochent aussi proche que désiré du nombre réel $l$.
Sur le schéma, on remarque qu’au bout d’un certain rang $n$, les termes se rapprochent de $l$.
On dit alors que $(u_n)$ converge vers $l$ et on note $\lim \limits_{n \to +\infty} u_n = l$.
Si $(u_n)$ n’admet pas de limite finie ou aucune limite, alors $(u_n)$ est dite divergente.
Exemples :
$\lim \limits_{n \to +\infty} n^2 = +\infty$. La suite $u_n = n^2$ est divergente.
$\lim \limits_{n \to +\infty} \sqrt{n} = +\infty$. La suite $u_n = \sqrt{n} $ est divergente.
$\lim \limits_{n \to +\infty} \dfrac{1}{n} = 0$. La suite $u_n = \dfrac{1}{n}$ est convergente.
$\lim \limits_{n \to +\infty} 3 + \dfrac{1}{n} = 3$. La suite $u_n = 3+ \dfrac{1}{n}$ est convergente.
La suite $(u_n)$ définie pour tout entier naturel $n$ par $u_n = (-1)^n$ prend successivement les valeurs $-1$ et $1$ selon que $n$ soit impaire ou paire.
Les valeurs de la suite ne peuvent donc pas se rapprocher dans un petit intervalle autour d’un nombre réel.
Ainsi la suite $u_n = (-1)^n$ n’admet pas de limite : c’est une suite divergente.
Opérations sur les limites
Opération sur les limites
Introduction
On commence par appliquer les règles d’opérations sur les limites à l’aide d’exemples.
$\lim \limits_{n \to +\infty} \dfrac{3}{-2 + \sqrt{n}}$.
$ \left. \begin{array}{l} \lim \limits_{n \to +\infty} \sqrt{n} = +\infty \\ \lim \limits_{n \to +\infty} -2 = -2 \end{array} \right \} \lim \limits_{n \to +\infty} – 2 + \sqrt{n} = +\infty$ par somme de limites
$\lim \limits_{n \to +\infty} 3 = 3$
Donc $\lim \limits_{n \to +\infty} \dfrac{3}{-2 + \sqrt{n}} = 0$ par quotient de limites
$\lim \limits_{n \to +\infty} -n^3 + 2$.
$ \left. \begin{array}{l} \lim \limits_{n \to +\infty} n^3 = +\infty \\ \lim \limits_{n \to +\infty} -1 = -1 \end{array} \right \} \lim \limits_{n \to +\infty} – n^3= -\infty$ par produit de limites
$\lim \limits_{n \to +\infty} 2 = 2$
Donc $\lim \limits_{n \to +\infty} -n^3 + 2 = -\infty $ par somme de limites.
$\lim \limits_{n \to +\infty} 2 + \dfrac{1}{n}$.
$ \left. \begin{array}{l} \lim \limits_{n \to +\infty} 2= 2 \\ \lim \limits_{n \to +\infty} \dfrac{1}{n}= 0 \end{array} \right \} \lim \limits_{n \to +\infty} 2 + \dfrac{1}{n} =2 + 0 = 2$ par somme de limites
Dans certains cas, il n’est pas possible d’appliquer les théorèmes d’opérations sur les limites, comme par exemple pour une forme indéterminée. Il existe cependant d’autres théorèmes pour pouvoir calculer ces limites.
Théorème de comparaison
Soient $(u_n)$ et $(v_n)$ deux suites,
Si à partir d’un certain rang $u_n \leq v_n$ et $\lim \limits_{n\to +\infty} u_n = +\infty$ alors $\lim \limits_{n \to + \infty} v_n = +\infty$.
De même, si à partir d’un certain rang $u_n \leq v_n$ et $\lim \limits_{n\to +\infty} v_n = -\infty$ alors $\lim \limits_{n \to + \infty} u_n = -\infty$.
Exemple :
Montrons que $n^2 -2n + 2 \geq (n – 1)^2$ et en déduire la limite de $u_n = n^2 – 2n + 2$.
Soit $n \in \mathbb{N}$,
$n^2 -2n + 2 \geq (n – 1)^2$
$\iff n^2 – 2n + 2 \geq n^2 -2n + 1$
$\iff 2 \geq 1$
On vient donc de montrer le résultat en raisonnant par équivalence.
Or $\lim \limits_{n \to +\infty} (n – 1)^2 = + \infty$, d’après le théorème de comparaison, $\lim \limits_{n \to + \infty} u_n = +\infty$
Théorème des gendarmes
Soient $(u_n)$, $(v_n)$ et $(w_n)$ trois suites,
Si à partir d’un certain rang $u_n \leq v_n \leq w_n$ et $\lim \limits_{n \to +\infty} u_n = \lim \limits_{n \to +\infty} w_n = l$, alors $\lim \limits_{n \to +\infty} v_n = l$.
Il s’agit donc d’un théorème d’encadrement.
Exemple :
Soit $a_n = 2 + \dfrac{(-1)^n}{n}$,
On ne peut ici pas appliquer directement les opérations sur les limites car $(-1)^n$ n’en admet pas.
On peut cependant remarquer que $(-1)^n$ oscille entre $-1$ et $1$.
Soit $n \in \mathbb{N}$,
$-1 \leq (-1)^n \leq 1$
$- \dfrac{1}{n} \leq \dfrac{(-1)^n}{n} \leq \dfrac{1}{n}$
$2 – \dfrac{1}{n} \leq 2 + \dfrac{(-1)^n}{n} \leq 2 + \dfrac{1}{n}$
$2 – \dfrac{1}{n} \leq a_n \leq 2 + \dfrac{1}{n}$
Or $\lim \limits_{n \to + \infty} 2 – \dfrac{1}{n} = 2 + \dfrac{1}{n} = 2$.
D’après le théorème des gendarmes, $\lim \limits_{n \to + \infty} a_n = 2$