Produit scalaire dans l'espace
Produit scalaire dans l’espace
Rappel : Vecteurs colinéaires
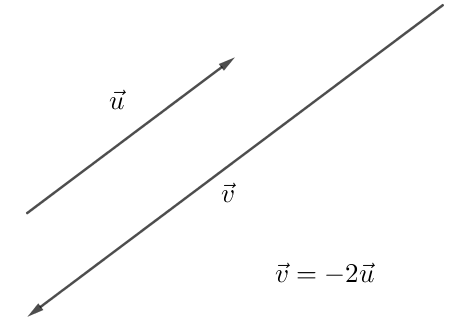
Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires si et seulement si il existe un réel $\lambda$ tel que $\overrightarrow{u}=\lambda\overrightarrow{v}$.
Exemple :
Propriétés
Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ colinéaires et non nuls ont la même direction.
Trois points $A$, $B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.
Le vecteur nul est colinéaire à tout autre vecteur.
Exemple
Les vecteurs $\overrightarrow{u}(2;3;1)$ et $\overrightarrow{v}(-6;9;-3)$ sont colinéaires car $\overrightarrow{v}=-3\times\overrightarrow{u}$.
Les vecteurs $\overrightarrow{u}(2;-3;1)$ et $\overrightarrow{v}(4;-6;-2)$ ne sont pas colinéaires car
$2\times 2=4$ ; $2\times(-3)=-6$ mais $2\times 1\neq -2$.
Produit scalaire, Définition
Dans l’espace, une unité de longueur étant choisie, on a pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$:
$\overrightarrow{u}.\overrightarrow{v}=\dfrac{1}{2}(||\overrightarrow{u}||^2+||\overrightarrow{v} ||^2-||\overrightarrow{u}-\overrightarrow{v} ||^2)$.
Coordonnées
On considère les deux vecteurs $\overrightarrow{u}(x;y;z)$ et $\overrightarrow{v}(x’;y’;z’)$, le produit scalaire de $\overrightarrow{u}$ et de $\overrightarrow{v}$ est le réel :
$\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’$.
Théorème
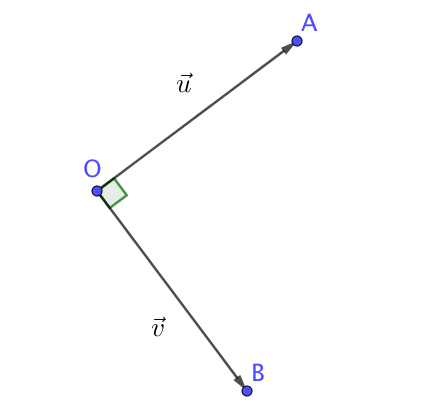
Soient deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non nuls et trois points $O$, $A$ et $B$ tels que $\overrightarrow{u}=\overrightarrow{OA}$ et $\overrightarrow{v}=\overrightarrow{OB}$.
Les trois propositions suivantes sont équivalentes :
$(OA)$ et $(OB)$ sont perpendiculaires,
$\overrightarrow{u}\cdot\overrightarrow{v}=0$
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux : on notera $\overrightarrow{u}\bot\overrightarrow{v}$.
Exemple
On considère les vecteurs $\overrightarrow{u}(1;3;1)$ et $\overrightarrow{v}(4;1;-7)$.
Sont-ils orthogonaux ?
Correction
On calcule leur produit scalaire :
$\overrightarrow{u}.\overrightarrow{v}=1\times 4+3\times1+1\times (-7)=0$
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont donc orthogonaux car leur produit scalaire est nul.
Équation paramétrique d'une droite
Système d’équations paramétriques d’une droite
Définition
Soit une droite $D$ définie par un point $A(x_A;y_A;z_A)$ et un vecteur directeur $\overrightarrow{u}(\alpha;\beta;\gamma)$ non nul.
Un point $M(x;y;z)$ appartient à $D$ si et seulement si les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{u}$ sont colinéaires.
C’est-à-dire s’il existe un réel $k$ tel que $\overrightarrow{AM}=k\overrightarrow{u}$.
On traduit cette égalité par un système d’équations paramétriques de la droite $D$:
\(D\left\{ \begin{array}{ll}x-x_A=k\alpha \\y-y_A=k\beta \\z-z_A=k\gamma\end{array} \right. \) avec $k \in \mathbb{R}$
Exemple
Soit $\Delta$ la droite passant par $A$ et de vecteur directeur $\overrightarrow{u}$, avec $\overrightarrow{u} (-2;-1;3)$ et $A(3;4;-5)$.
Donner un système d’équations paramétriques de $\Delta$
Correction
On définit un système d’équations paramétriques de $\Delta$ à partir des coordonnées du vecteur $\overrightarrow{u}$ et du point $A$.
\(\Delta\left\{ \begin{array}{ll}x-3=k(-2) \\y-4=-k \\z+5=3k\end{array} \right. \) avec $k \in \mathbb{R}$
$\iff$ \(\Delta\left\{ \begin{array}{ll}x=3-2k \\y=-k+4 \\z=3k-5\end{array} \right. \) avec $k \in \mathbb{R}$
Équation cartésienne d'un plan
Equation cartésienne d’un plan
Définition
Soient $a,b,c$ et $d$ quatre réels avec $a,b$ et $c$ tous nuls.
$\mathcal{P} :ax+by+cz+d=0$ est l’équation cartésienne d’un plan de l’espace.
Propriété
Tout plan $\mathcal{P}$ d’équation $ax+by+cz+d=0$ admet un vecteur normal non nul $\overrightarrow{n}(a;b;c)$.
La réciproque est vraie.

Exemples
1) Déterminer l’équation cartésienne du plan $\mathcal{P}$ passant par $A(4;0;-1)$ et normal à $\overrightarrow{n}(2;-1;3)$.
2) Soit $\mathcal{P}: 2x-4y+6z-9=0$.
Déterminer un vecteur $\overrightarrow{n}$ normal à $\mathcal{P}$ et un point $A$ du plan
Correction
- 1) Etape 1 : On définit l’équation cartésienne du plan à partir des coordonnées du vecteur $\overrightarrow{n}$.
On a: $\mathcal{P} : 2x-y+3z+d=0$.
- Etape 2 : On sait que $A \in \mathcal{P} $, on remplace $x, y$ et $z$ par les coordonnées du point $A$ appartenant au plan.
$2(4)-0+3(-1)+d=0$
- Etape 3 : On en déduit la valeur de $d$ et ainsi l’équation cartésienne du plan $\mathcal{P}$.
$d=-5$
On conclut que: $\mathcal{P} :2x-y+3z-5=0$.
- 2) Etape 1 : On définit un vecteur $\overrightarrow{n}$ normal à $\mathcal{P}$ à partir des coefficients de $x,y$ et $z$ de l’équation cartésienne.
$\overrightarrow{n}(2;-4;6)$ ou encore $\overrightarrow{n’}(1;-2;3)$ sont deux vecteurs normaux.
- Etape 2 : On fixe deux des trois inconnues afin de calculer les coordonnées pour que le point $A$ appartienne au plan.
On pose : $x=1$ et $y=2$ , avec $A \in \mathcal{P} $, on remplace : $2-8+6z-9=0$. $z=\dfrac{15}{6}=\dfrac{5}{2}$
On a alors : $A\left(1;2;\dfrac{5}{2}\right)$
Distance d'un point à un plan / à une droite
Ces notions ne sont pas exigibles au programme :
– Soient le plan \(P\) d’équation \(ax + by + cz + d = 0\) et un point \(A (x_A; y_A; z_A)\).
La distance du point au plan se calcule par :
\(D(A, P) = AH = \dfrac{|ax_A + by_A + cz_A + d|}{\sqrt{a^2 + b^2 + c^2}}\)
– La distance du point $A$ à une droite \(\Delta\) est la distance \(AH\) telle que :
\( \left\{ \begin{array}{ll} H \in \Delta \\ \overrightarrow{AH} . \overrightarrow{u} = 0 \end{array} \right. \)
$\overrightarrow{u}$ étant une vecteur directeur de la droite$\Delta$
Projection orthogonale
Projection orthogonale dans l’espace
Sur un plan : définition
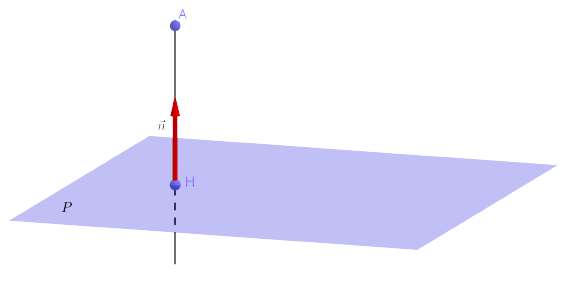
Le projeté d’un point \(A\) sur un plan est le point \(H\) du plan tel que \(\overrightarrow{AH}\) est orthogonal au plan.
Sur une droite : définition
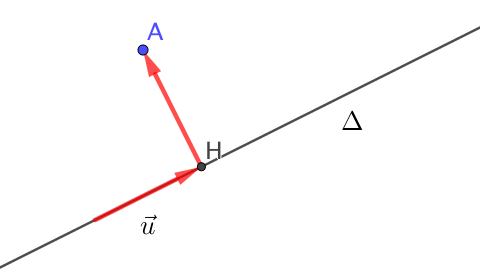
Le projeté orthogonal d’un point \(A\) sur une droite \(\Delta\) est le point \(H\) vérifiant :
\( \left\{ \begin{array}{ll} H \in \Delta \\ \overrightarrow{AH} . \overrightarrow{u} = 0 \end{array} \right. \)
où \(\overrightarrow{u}\) est un vecteur directeur de la droite \(\Delta\).