Loi à densité sur [a ; b]
Lois de probabilité continues
Définition : Densité de probabilité sur un intervalle $[a;b]$
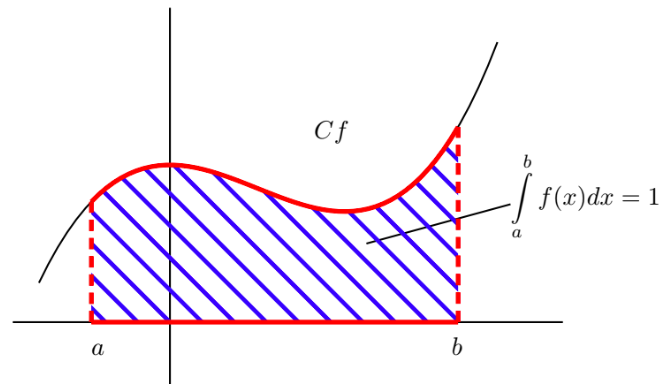
Soit $f$ une fonction continue et positive sur un intervalle $[a;b]$.
$f$ est une densité de probabilité sur $[a;b]$ si et seulement si :
$ \displaystyle \int \limits_a^{b}f(x)dx=1$
Exemple
Soit $ \displaystyle f(x)=\frac{2}{x^2}$ définie sur $[1 ; 2]$.
Cette fonction $f$ est-elle une densité de probabilité ?
Correction
$f$ est continue et positive sur $[1;2]$. On intègre la fonction entre $1$ et $2$:
\( \displaystyle \int \limits_{1} ^{2}\frac{2}{x^2} dx=\left[ -\frac{2}{x}\right]_{1}^2\)
\( \displaystyle \int \limits_{1} ^{2}\frac{2}{x^2} dx= -\frac{2}{2}+\frac{2}{1} = 1\)
On a donc: \( \displaystyle \int \limits_{1} ^{2} f(x) dx= 1\)
Cette intégrale vaut $1$ donc la fonction $f$ est bien une densité de probabilité sur $[1;2]$.
Loi uniforme sur [a ; b]
Loi uniforme sur un intervalle $[a;b]$
Définition
$X$, une variable aléatoire suit une loi uniforme sur $[a;b]$ si et seulement si la fonction de densité de probabilité est :
\( \displaystyle f(x)=\frac{1}{b-a}\).
On vérifie que \( \displaystyle \int \limits_a^{b}f(x)dx=1\).
Propriétés
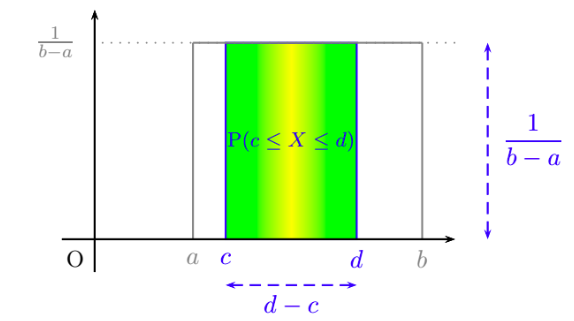
Pour tout intervalle $[c;d]$ inclus dans $[a;b]$, on a:
\( \displaystyle P(c\leqslant X \leqslant d)=\frac{d-c}{b-a}\).
Exemple
1) On choisit un nombre réel au hasard dans l’intervalle $[0 ;5]$. On note $X$ la variable aléatoire égale au nombre choisi.
a)Quelle est la probabilité que ce nombre soit supérieur à 4 ?
b)Compris entre $e$ et $\pi$ ?
Correction
1 a) $X$ suit la loi uniforme sur $[0;5]$. La probabilité que ce nombre soit supérieur à 4 est :
$P(X > 4) = P( 4 < X\leq 5)=\displaystyle\frac{5-4}{ 5-0}=\displaystyle\frac{1}{ 5}$
1 b) La probabilité que ce nombre soit compris entre $e$ et $\pi$ est :
$\displaystyle P(e \leqslant X \leqslant \pi) = \frac{\pi – e}{5-0} \approx 0, 085$
Espérance mathématique – Propriétés
Si $X$ suit une loi uniforme sur un intervalle $I = [a; b]$, alors son espérance mathématique vaut :
\( \displaystyle E(X)=\int \limits_a^{b}tf(t)dt= \int \limits_a^{b}t\times \frac{1}{b-a}dt \)
Soit après calcul :
\( \displaystyle E(X)=\frac{a+b}{2}\).
Remarque :
Dans l’exercice précédent, on trouve : $E(X) =\displaystyle \frac{0+5}{2}= 2,5$.

