Equations et nombres complexes
Résolution d’équations avec des nombres complexes
Equations du premier degré
Il y a deux formes d’équations du premier degré avec solutions complexes :
$\bullet$ $az+b=0$ avec $a$ et $b$ dans $\mathbb{C}$, dont la résolution se fait comme pour une équation du premier degré avec des réels.
$\bullet$ $az+b\bar z +c=0$ avec $a$, $b$ et $c$ dans $\mathbb{C}$ dont la résolution se fait en remplaçant $z$ par sa forme algébrique : $z=a+ib$.
Exemple
Trouver la ou les solutions de l’équation $(E) : z-\bar z+i=0$.
On pose $z=a+ib$ la forme algébrique de $z$. On remplace cette forme algébrique de $z$ dans l’équation $(E)$ :
$(a+ib)-\overline{(a+ib)}+i=0 \Leftrightarrow a+ib-(a-ib)+i=0 \Leftrightarrow 2ib=-i \Leftrightarrow b=-\dfrac12$
Ainsi, les solutions de $(E)$ sont tous les nombres complexes s’écrivant :
$z=a-\dfrac12 i$, avec $a$ réel.
Equations du second degré
La forme générale d’une équation du second degré est la suivante :
$\boxed{az^2+bz+c=0}$ avec $a$, $b$ et $c$ réels.
La résolution de cette équation est semblable à celle d’une équation du second degré avec des réels, c’est-à-dire qu’il s’agit de calculer le discriminant de l’équation :
$\Delta=b^2-4ac$
Il y aura tout de même des solutions dans le cas du discriminant négatif :
$\bullet$ Si $\Delta >0$, les deux solutions réelles sont : $z_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $z_2=\dfrac{-b-\sqrt{\Delta}}{2a}$.
$\bullet$ Si $\Delta=0$, la solution est $z_0=-\dfrac{b}{2a}$.
$\bullet$ Si $\Delta<0$,les deux solutions complexes sont : $z_1=\dfrac{-b+i\sqrt{-\Delta}}{2a}$ et $z_2=\dfrac{-b-i\sqrt{-\Delta}}{2a}$.
Exemple
Trouver les solutions de l’équation : $(F) : z^2+4z+\dfrac{25}{4}=0$.
On a $\Delta = 16-25=-9 <0$ donc les deux solutions sont :
$z_1=\dfrac{-4+3i}{2}$ et $z_2=\dfrac{-4-3i}{2}$.
Modules et arguments
Module et argument
Module
On considère un nombre complexe $z=a+ib$ et on note $M$ le point du plan complexe d’affixe $z$.
On définit le module de $z$ (qu’on note $|z|$) par la distance du point $M$ au point d’origine $O$.
On a alors la formule suivante :
$|z|=OM =\sqrt{a^2+b^2}$
Argument
On note $\overrightarrow{u}$ le vecteur directeur de norme $1$ de l’axe des réels.
On définit alors l’argument d’un nombre complexe $z=a+ib$ (affixe du point $M$ dans le plan complexe) l’angle formé par le vecteur $\overrightarrow{u}$ et le vecteur $\overrightarrow{OM}$.
On écrit alors :
$ \operatorname{arg} (z) = (\overrightarrow{u}, \overrightarrow{OM} ) ~ [2\pi]$
En notant $\theta = \operatorname{arg}(z)~ [2\pi]$ alors on a les égalités suivantes :
- $\cos(\theta)=\dfrac{a}{|z|}$
- $\sin(\theta)=\dfrac{b}{|z|}$
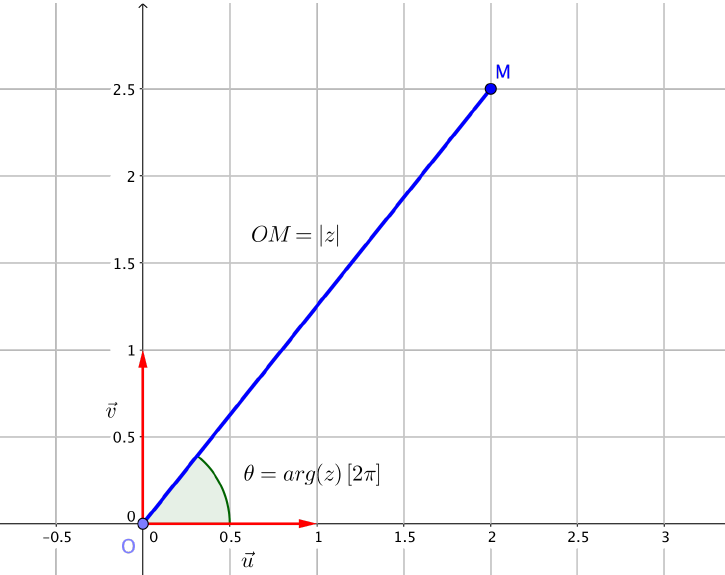
Illustration graphique
L’angle $\theta$ est ici un argument de $z$ : $\operatorname{arg}(z)=\theta ~ [2\pi]$.
Exemple
Calculer le module et un argument de $z_1=1+i$ et $z_2=4-4i$.
$z_1$ s’Ècrit : $z_1=a_1+ib_1$ avec $a_1=1$ et $b_1=1$ donc
$|z_1|=\sqrt{a_1^2+b_1^2}= \sqrt2$.
On note $\operatorname{arg}(z_1)=\theta_1 ~ [2\pi]$.
On a :
$\cos(\theta_1)=\dfrac{1}{\sqrt2}=\dfrac{\sqrt2}{2}$ et $\sin(\theta_1)$
$\cos(\theta_1)= \dfrac{1}{\sqrt2}=\dfrac{\sqrt2}{2}$.
Conclusion : $\theta_1=\dfrac{\pi}{4}~ [2\pi]$.
$z_2$ s’écrit : $z_2=a_2+ib_2$ avec $a_2=4$ et $b_2=-4$ donc
$|z_2|=\sqrt{a_2^2+b_2^2}=$
$|z_2|=\sqrt{16+16}=4\sqrt{2}$.
On note $\operatorname{arg}(z_2)=\theta_2 ~ [2\pi]$.
On a :
- $\cos(\theta_2)=\dfrac{4}{4\sqrt{2}}=\dfrac{\sqrt2}{2} $
- $\sin(\theta_2)= \dfrac{-4}{4\sqrt{2}}=-\dfrac{\sqrt2}{2}$.
Conclusion : $\theta_2=-\dfrac{\pi}{4}~ [2\pi]$.
Argument et angle formé par deux vecteurs
A savoir par coeur :
Soient \(A(z_A), B(z_B), C(z_C), D(z_D)\) quatre points d’un plan complexe.
\(arg \left(\dfrac{z_D – z_C}{z_B – z_A}\right) = (\overrightarrow{AB} ; \overrightarrow{CD}) [2\pi]\)
Ainsi \( arg \left(\dfrac{z_D – z_C}{z_B – z_A}\right)\) est égal à l’angle formé entre les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) modulo \(2\pi\).
Caractérisation de nombres complexes
Caractérisations des nombres complexes
Réels et imaginaires purs
Soit $z=a+ib$ un nombre complexe quelconque.
On dit que $z$ est réel lorsque $b=0$ et que $z$ est imaginaire pur lorsque $a=0$.
Exemple
- $2i$ est imaginaire pur,
- $3$ est réel
- $3+2i$ n’est ni réel, ni imaginaire pur.
Caractérisation avec les parties réelles et imaginaires
On constate simplement que si $z$ est un nombre complexe non nul, $\boxed{z\in \mathbb{R} \Leftrightarrow Im(z)=0}$.
Autrement dit, $z$ est réel si et seulement si sa partie imaginaire est nulle.
De même, $z$ est imaginaire pur si et seulement si sa partie réelle est nulle : $\boxed{z\in i\mathbb{R} \Leftrightarrow Re(z)=0}$.
Caractérisation avec l’argument
Soit $z$ un nombre complexe non nul.
$\bullet$ $z$ est réel si et seulement si $arg(z)=k\pi$ avec $k\in \mathbb{Z}$.
$\bullet$ $z$ est imaginaire pur si et seulement si $arg(z)=\dfrac{\pi}{2}+k\pi$ avec $k\in \mathbb{Z}$.
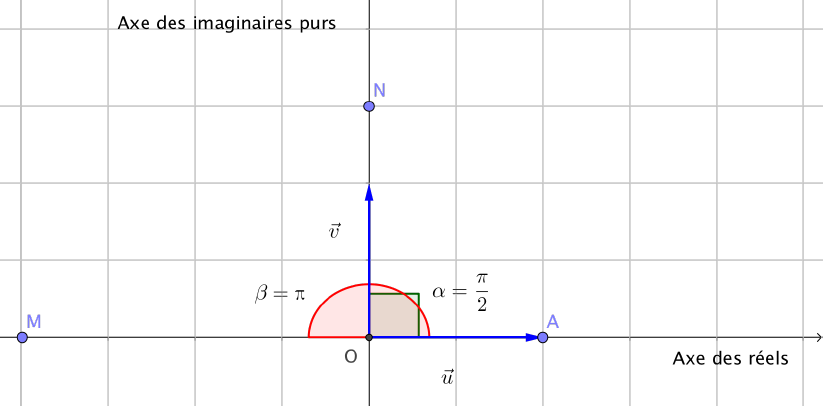
Illustration graphique
L’affixe du point $M$ est un réel négatif, tandis que l’affixe du point $N$ est imaginaire pur.
le point $A$ a un affixe réel égal à $1$.
Propriétés des modules et arguments
Propriétés des modules et arguments
Module
Soient $z$ et $z’$ deux nombres complexes (avec $z’$ non nul).
On a les propriétés suivantes :
$\bullet $ $|z\times z’|=|z|\times |z’| $
$\bullet $ $ |z^n|=|z|^n$ pour $n\in \mathbb{N}$
$\bullet$ $\left| \dfrac{z}{z’}\right| = \dfrac{|z|}{|z’|}$ si $z’\neq 0$
$\bullet$ $|z+z’| \leqslant |z|+|z’|$
Argument
Soient $z$ et $z’$ deux nombres complexes (avec $z’$ non nul).
On a les propriétés suivantes :
$\bullet $ $ arg(z\times z’)=arg(z)+arg(z’) ~ [2\pi]$
$\bullet $ $ arg(z^n)=n\times arg(z) ~ [2\pi]$ pour $n\in \mathbb{N}$
$\bullet$ $ arg\bigg(\dfrac{z}{z’}\bigg) = arg(z)-arg(z’) ~ [2\pi]$
Exemple
Soient $a=1+i$ et $b=2i$ deux nombres complexes.
Calculer le module de $a^4$ ainsi qu’un argument de $\dfrac{a}{b}$.
D’après les propriétés du module on a : $|a^4|=|a|^4$ donc on calcule $|a|=\sqrt{1^2+1^2}=\sqrt2$.
Finalement : $|a^4|=|a|^4=\sqrt2^4= 4$.
D’après les propriétés des arguments, on a : $arg\left(\dfrac{a}{b} \right)= arg(a)-arg(b)~ [2\pi]$.
Ici, on a : $a={\sqrt2}\left(\dfrac{\sqrt2}{2}+i\dfrac{\sqrt2}{2}\right)$ donc $arg(a)=\dfrac{\pi}{4}~ [2\pi]$.
De plus, comme $b$ est un imaginaire pur, $arg(b)=\dfrac{\pi}{2}~ [2\pi]$.
On en déduit que $arg\left(\dfrac{a}{b} \right)=\dfrac{\pi}{4}-\dfrac{\pi}{2}~ [2\pi]$.
Finalement : $arg\left(\dfrac{a}{b} \right)= -\dfrac{\pi}{4} ~ [2\pi]$
Forme trigonométrique et exponentielle - Propriétés
Propriétés des formes trigonométriques et exponentielles
Opérations sur l’exponentielle complexe
Module
Par définition, on a $e^{i\theta}=\cos(\theta)+i\sin(\theta)$ donc
$|e^{i\theta}|=\sqrt{\cos^2(\theta)+\sin^2(\theta)}=1$.
A retenir donc :Tout nombre complexe de la forme $e^{i\theta}$ se situe sur le cercle de centre $O$ et de rayon $1$, c’est-à-dire que son module vaut $1$.
Conjugué
Si $z=e^{i\theta}$ alors on a $\boxed{\bar z = e^{-i\theta}}$.
Périodicité et inverse
Les fonctions cosinus et sinus étant périodiques de période $2\pi$ on a, pour tout $k\in \mathbb{N}$ :
$\boxed{ e^{i(\theta+2k\pi)}=e^{i\theta}}$
On a, en outre, l’égalité suivante :
$\boxed{\dfrac{1}{e^{i\theta}}=e^{-i\theta}}$.
Produit et quotient
Si $\theta$ et un réel et $n$ un entier naturel, on a :
$\boxed{{(e^{i\theta})}^n=e^{in\theta}}$.
De manière plus générale, si $\theta$ et $\theta’$ sont des réels quelconques :
$\boxed{e^{i(\theta+\theta’)}=e^{i\theta}\times e^{i\theta’}}$.
Enfin, le quotient de deux exponentielles complexes donne le résultat suivant :
$\boxed{\dfrac{e^{i\theta}}{e^{i\theta’}}=e^{i(\theta-\theta’)}}$.
Exemple
On définit les deux nombres complexes $a=1+i$ et $b=2i$.
Calculer la forme exponentielle de $a$ puis de $b$ et en déduire celle de $a\times b$ et celle de $\dfrac{\bar a}{b}$.
En utilisant les méthodes vues dans les vidéos précédentes, on trouve aisément :
$a=\sqrt2 e^{i\frac{\pi}{4}}$ et
$b=2e^{i\frac{\pi}{2}}$.
On en déduit avec les formules de la notation exponentielle que:
$a\cdot b = 2\sqrt2 e^{i(\frac{\pi}{2}+\frac{\pi}{4})} $
$a\cdot b = 2\sqrt2 e^{i\frac{3\pi}{4}}$
De même, on a :
$\bar a = \sqrt2 e^{-i\frac{\pi}{4}}$ donc
$\dfrac{\bar a}{b}= \dfrac{\sqrt2}{2}e^{i(-\frac{\pi}{4}-\frac{\pi}{2})}$
$\dfrac{\bar a}{b}= \dfrac{\sqrt2}{2}e^{-i\frac{3\pi}{4}}$.