Modules et arguments
Module et argument
Module
On considère un nombre complexe $z=a+ib$ et on note $M$ le point du plan complexe d’affixe $z$.
On définit le module de $z$ (qu’on note $|z|$) par la distance du point $M$ au point d’origine $O$.
On a alors la formule suivante :
$|z|=OM =\sqrt{a^2+b^2}$
Argument
On note $\overrightarrow{u}$ le vecteur directeur de norme $1$ de l’axe des réels.
On définit alors l’argument d’un nombre complexe $z=a+ib$ (affixe du point $M$ dans le plan complexe) l’angle formé par le vecteur $\overrightarrow{u}$ et le vecteur $\overrightarrow{OM}$.
On écrit alors :
$ \operatorname{arg} (z) = (\overrightarrow{u}, \overrightarrow{OM} ) ~ [2\pi]$
En notant $\theta = \operatorname{arg}(z)~ [2\pi]$ alors on a les égalités suivantes :
- $\cos(\theta)=\dfrac{a}{|z|}$
- $\sin(\theta)=\dfrac{b}{|z|}$
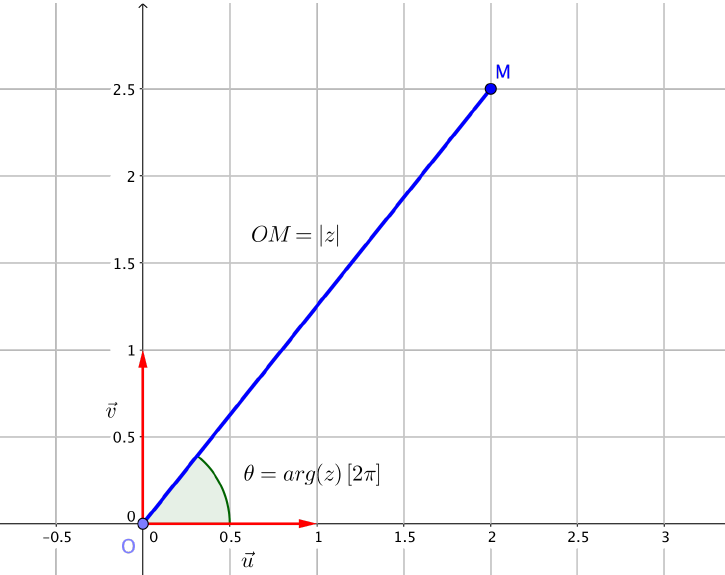
Illustration graphique
L’angle $\theta$ est ici un argument de $z$ : $\operatorname{arg}(z)=\theta ~ [2\pi]$.
Exemple
Calculer le module et un argument de $z_1=1+i$ et $z_2=4-4i$.
$z_1$ s’Ècrit : $z_1=a_1+ib_1$ avec $a_1=1$ et $b_1=1$ donc
$|z_1|=\sqrt{a_1^2+b_1^2}= \sqrt2$.
On note $\operatorname{arg}(z_1)=\theta_1 ~ [2\pi]$.
On a :
$\cos(\theta_1)=\dfrac{1}{\sqrt2}=\dfrac{\sqrt2}{2}$ et $\sin(\theta_1)$
$\cos(\theta_1)= \dfrac{1}{\sqrt2}=\dfrac{\sqrt2}{2}$.
Conclusion : $\theta_1=\dfrac{\pi}{4}~ [2\pi]$.
$z_2$ s’écrit : $z_2=a_2+ib_2$ avec $a_2=4$ et $b_2=-4$ donc
$|z_2|=\sqrt{a_2^2+b_2^2}=$
$|z_2|=\sqrt{16+16}=4\sqrt{2}$.
On note $\operatorname{arg}(z_2)=\theta_2 ~ [2\pi]$.
On a :
- $\cos(\theta_2)=\dfrac{4}{4\sqrt{2}}=\dfrac{\sqrt2}{2} $
- $\sin(\theta_2)= \dfrac{-4}{4\sqrt{2}}=-\dfrac{\sqrt2}{2}$.
Conclusion : $\theta_2=-\dfrac{\pi}{4}~ [2\pi]$.
Modules et arguments- Exercice 1
Exercice
Soit \( z = 3 – 3i\sqrt{3} \). On cherche \(\left| z \right|\) et \( arg(z) \).
Étape 1 : On calcule le module de \(z,\) \(\left| z \right|=\sqrt{a^2+b^2}\).
Étape 2 : On calcule le cosinus et le sinus de l’argument de z.
Étape 3 : On s’aide d’un cercle trigonométrique pour retrouver la valeur de l’argument à partir de son cosinus et de son sinus.
Modules et arguments- Exercice 2
Exercice
Calculons le module et l’argument de \( Z = (1 + i)^7 \)
Étape 1 : On pose \( z = 1 + i\) pour calculer son module et son argument.
Étape 2 : On calcule le module de z, \(\left| z \right| = \sqrt{a^2+b^2}\).
Étape 3 : On calcule le cosinus et le sinus de l’argument de z.
Étape 4 : On s’aide d’un cercle trigonométrique pour retrouver la valeur de l’argument à partir de son cosinus et de son sinus.
Étape 5 : D’après le cours, \( \left| z^7 \right| = \left| z \right|^7 \).
Étape 6 : On utilise la formule du cours \( arg(z^7) = 7 \times arg(z) \).
Propriétés des modules et arguments
Propriétés des modules et arguments
Module
Soient $z$ et $z’$ deux nombres complexes (avec $z’$ non nul).
On a les propriétés suivantes :
$\bullet $ $|z\times z’|=|z|\times |z’| $
$\bullet $ $ |z^n|=|z|^n$ pour $n\in \mathbb{N}$
$\bullet$ $\left| \dfrac{z}{z’}\right| = \dfrac{|z|}{|z’|}$ si $z’\neq 0$
$\bullet$ $|z+z’| \leqslant |z|+|z’|$
Argument
Soient $z$ et $z’$ deux nombres complexes (avec $z’$ non nul).
On a les propriétés suivantes :
$\bullet $ $ arg(z\times z’)=arg(z)+arg(z’) ~ [2\pi]$
$\bullet $ $ arg(z^n)=n\times arg(z) ~ [2\pi]$ pour $n\in \mathbb{N}$
$\bullet$ $ arg\bigg(\dfrac{z}{z’}\bigg) = arg(z)-arg(z’) ~ [2\pi]$
Exemple
Soient $a=1+i$ et $b=2i$ deux nombres complexes.
Calculer le module de $a^4$ ainsi qu’un argument de $\dfrac{a}{b}$.
D’après les propriétés du module on a : $|a^4|=|a|^4$ donc on calcule $|a|=\sqrt{1^2+1^2}=\sqrt2$.
Finalement : $|a^4|=|a|^4=\sqrt2^4= 4$.
D’après les propriétés des arguments, on a : $arg\left(\dfrac{a}{b} \right)= arg(a)-arg(b)~ [2\pi]$.
Ici, on a : $a={\sqrt2}\left(\dfrac{\sqrt2}{2}+i\dfrac{\sqrt2}{2}\right)$ donc $arg(a)=\dfrac{\pi}{4}~ [2\pi]$.
De plus, comme $b$ est un imaginaire pur, $arg(b)=\dfrac{\pi}{2}~ [2\pi]$.
On en déduit que $arg\left(\dfrac{a}{b} \right)=\dfrac{\pi}{4}-\dfrac{\pi}{2}~ [2\pi]$.
Finalement : $arg\left(\dfrac{a}{b} \right)= -\dfrac{\pi}{4} ~ [2\pi]$