Ensemble des nombres complexes de module 1
Ensemble $\mathbb{U}$ des nombres complexes de module $1$
Définition :
On désigne par $\mathbb{U}$ l’ensemble des nombres complexes de module $1$ c’est à dire l’ensemble $\{ z \in \mathbb{C}, |z| =1 \}$.
On peut citer en guise d’exemple les nombres suivants :
- $1 \in \mathbb{U}$
- $-1 \in \mathbb{U}$
- $e^{i\frac{\pi}{2}}=i \in \mathbb{U}$
- $e^{-i\frac{\pi}{2}}=-i \in \mathbb{U}$
On pourra remarquer que $0 \notin \mathbb{U}$.
On s’intéresse à l’image de l’ensemble $\mathbb{U}$ dans le plan complexe, c’est à dire, la représentation géométrique de cet ensemble.
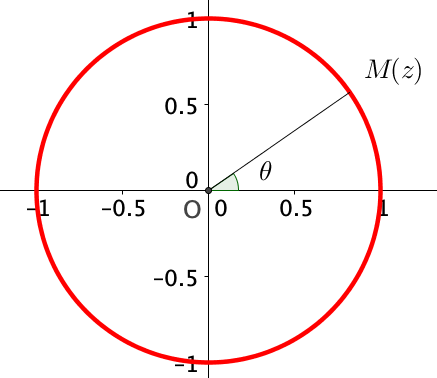
Ainsi, l’image d’un nombre complexe de module $1$ dans le plan complexe est un point du cercle trigonométrique, c’est à dire un point du cercle de rayon 1.
On dira alors que pour tout $z \in \mathbb{U}$, il existe un unique $\theta \in ]-\pi, \pi]$ tel que
$z = e^{i\theta}$.
On admet alors que l’image de $\mathbb{U}$ dans le plan complexe est le cercle trigonométrique.
Propriétés
Propriété 1 :
Soit $z \in \mathbb{C}^*$,
$z$ appartient à l’ensemble $\mathbb{U}$ si et seulement si $\overline{z} = \dfrac{1}{z}$.
Démonstration :
Soit $z \in \mathbb{C}^*$,
si $z$ appartient à l’ensemble $\mathbb{U}$ alors $|z| = 1$ ou encore $|z|^2 = 1$
C’est à dire $z\overline{z} = 1$ d’où $\overline{z} = \dfrac{1}{z}$.
Réciproquement, si $\overline{z} = \dfrac{1}{z}$ alors $z\overline{z} = 1$ c’est à dire $|z|^2 = 1$ donc $z \in \mathbb{U}$.
Propriété 2 :
Soit $(z_1, z_2) \in \mathbb{U}^2$ alors le produit $z_1 z_2$ appartient à $\mathbb{U}^2$ .
On dit alors que l’ensemble $\mathbb{U}$ est stable par la multiplication.
Démonstration:
Soit $(z_1, z_2) \in \mathbb{U}^2$
$|z_1 z_2| = |z_1|\times| z_2| = 1 \times 1 = 1$
Ainsi $z_1 z_2\in \mathbb{U}$
Propriété 3
Soit $z \in \mathbb{U}$ alors l’inverse de $z$ appartient aussi à l’ensemble $\mathbb{U}$.
On dira que l’ensemble $\mathbb{U}$ est stable par passage à l’inverse.
Démonstration :
Soit $z \in \mathbb{U}$ alors $z \neq 0$,
En outre,
$\left | \dfrac{1}{z} \right | = \dfrac{1}{|z|} = 1$ donc
$\dfrac{1}{z} \in \mathbb{U}$.
Interprétation géométrique de la multiplication d’un nombre complexe par un nombre $u \in \mathbb{U}$.
On sait qu’il existe $\theta \in ]-\pi, \pi]$ tel que $ u = e^{i\theta}$.
On considère un nombre complexe quelconque $z$. On sait que l’on peut écrire ce dernier sous la forme
$z = \rho e^{i\alpha}$.
On s’intéresse désormais à l’image dans le plan complexe du produit
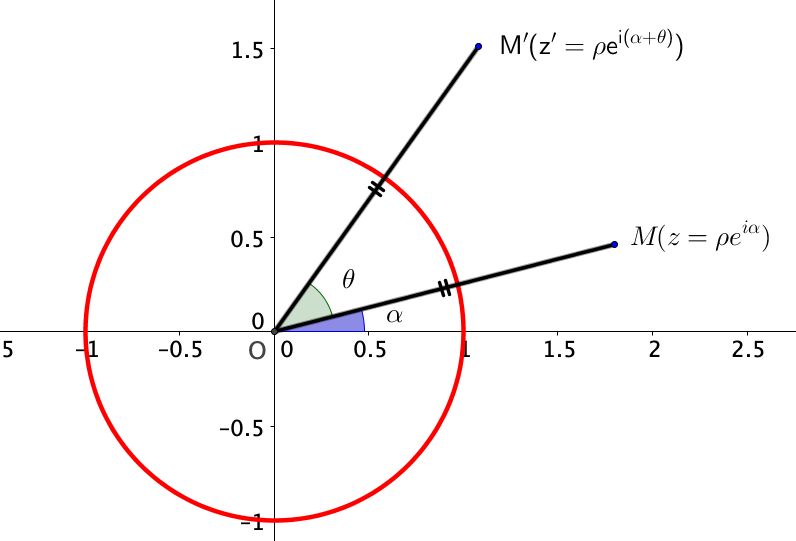
$z \times u = \rho e^{i\alpha} \times e^{i\theta} = \rho e^{i(\alpha +\theta)}$.
Le module de l’image du nombre ainsi formé est de même module que $z$ : il faut $\rho$ et son angle vaut $\alpha +\theta$ : on a donc tourné d’un angle $\theta$.
Ainsi, l’image du point $M$ d’affixe $z$ par le produit par $u \in \mathbb{U}$ est le point $M’$ d’affixe $z’$, avec $M’$ obtenu par rotation autour du point O d’un angle $\theta$ à partir du point $M$.
La transformation géométrique correspondant à cette opération dans le plan complexe consistant à multiplier un nombre complexe par un nombre complexe de module 1 est une rotation de centre $O$ et d’angle $\theta$, c’est à dire un argument du nombre complexe de module 1.
Finalement, on considère un nombre complexe quelconque $z$ non nul.
Alors $\dfrac{z}{|z|}$ appartient à $\mathbb{U}$.
En effet, $\left |\dfrac{z}{|z|}\right | = \dfrac{|z|}{|z|} = 1$.
Le point d’affixe M $\dfrac{z}{|z|}$ se situe à l’intersection du cercle trigonométrique et du segment $[OM]$.


