- 1Définition des nombres complexes
- 2Définition des nombres complexes- Exercice
- 3Égalité de complexes, conjugué, opérations élémentaires
- 4Égalité de complexes, conjugué, opérations élémentaires - Exercice 1
- 5Égalité de complexes, conjugué, opérations élémentaires- Exercice 2
- 6Nombres complexes : Conjugué d'un produit, d'un inverse, d'une puissance, démonstration
Définition des nombres complexes
Définition des nombres complexes
L’ensemble $\mathbb{C}$
Un nombre complexe $z$ se présente sous la forme $z=a+i b$ où $a$ et $b$ sont réels et $i$ est tel que $i^2=-1$.
On appelle $a$ la partie réelle de $z$ et on note : $\mathcal{Re}(z)=a$.
On appelle $b$ la partie imaginaire de $z$ et on note : $\mathcal{Im}(z)=b$.
On note alors $\mathbb{C}$ l’ensemble des nombres complexes : $$ \mathbb{C}= \{a+ib ~|~ a,b\in \mathbb{R}\} $$
Illustration graphique
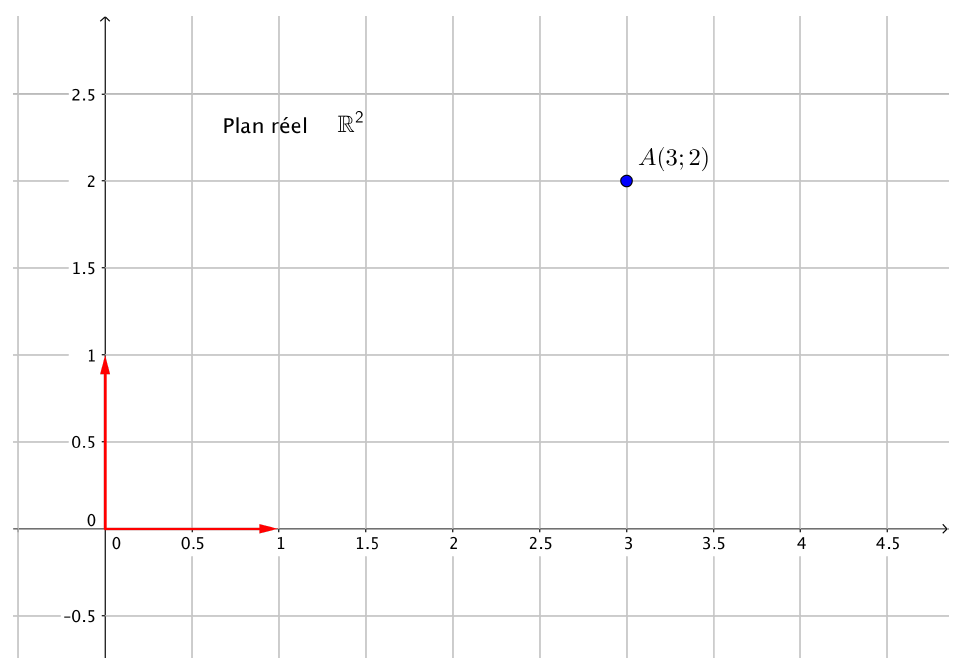
Plan réel :
Plan complexe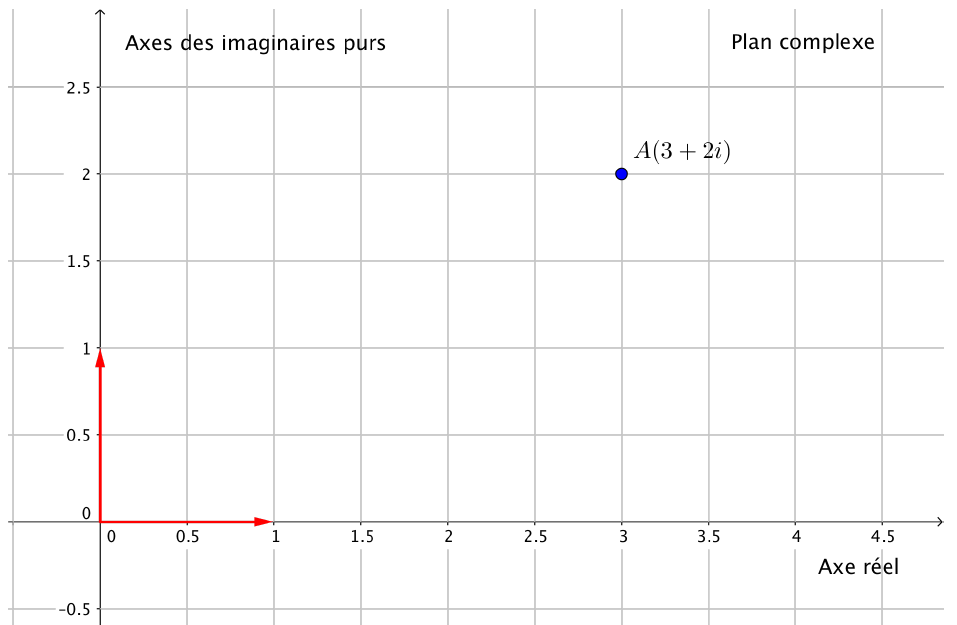
Le point $A$ est représenté par le nombre complexe $z=3+2i$ dans le plan complexe.
On parle d’affixe dans le plan complexe et de coordonnées dans le plan réel.
On dit que $z$ est l’affixe du point $A$ et on note $A(3+2i)$
Définition des nombres complexes- Exercice
À savoir faire :
Étape 1 : On place le point dans le repère en plaçant la partie réelle de l’affixe sur l’axe des abscisses.
Étape 2 : On place ensuite la partie imaginaire de l’affixe sur l’axe des ordonnées.
Égalité de complexes, conjugué, opérations élémentaires
Egalité de complexes, conjugués, opérations élémentaires
Egalité de nombres complexes
On dit que deux nombres complexes $z=a+ib$ et $z’=a’+ib’$ sont égaux si et seulement si $a=a’$ et $b=b’$.
Opérations élémentaires
Les opérations de sommes, différences, multiplications et divisions existent dans $\mathbb{C}$.
Pour $z=a+ib$ et $z’=a’+ib’$ deux nombres complexes alors :
$\bullet$ $z+z’ = (a+a’)+i (b+b’)$
$\bullet$ $z\cdot z’ = (a+ib)\cdot (a’+ib’) = (aa’-bb’) + i (a’b+ab’)$
Conjugué d’un nombre complexe
On considère un nombre complexe quelconque $z=a+ib$ avec $a\in \mathbb{R}$ et $b\in\mathbb{R}$.
On appelle conjugué de $z$ et on note $\bar z$ le nombre $a-ib$.
Exemple : si $z=1,5+i$ alors $\bar z = 1,5-i$.
Illustration graphique
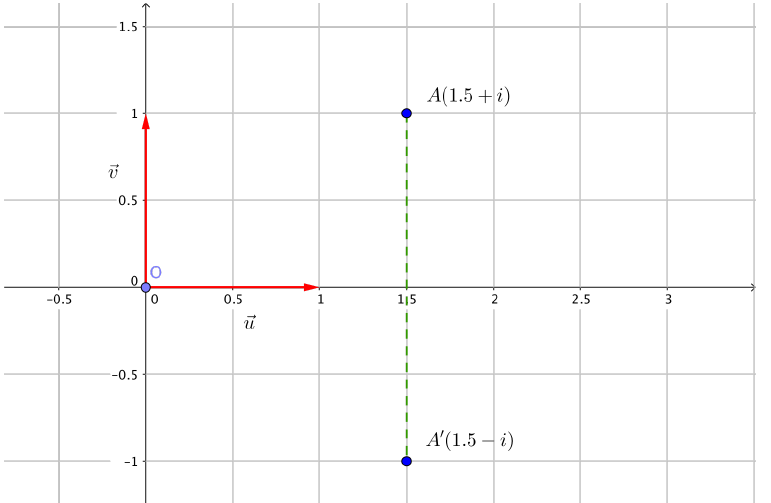
Le point $A’$ d’affixe $\bar z$ est le symétrique du point $A$ d’affixe $z$ par rapport à l’axe des abscisses
Propriétés des conjugués
si $z$ et $z’$ sont deux nombres complexes (avec $z’$ non nul), alors :
$\bullet $ $\overline{z+z’} = \bar z + \bar{z’}$
$\bullet $ $\overline{zz’} = \bar z \cdot \bar z’$
$\bullet$ $\overline{\left(\dfrac{z}{z’}\right)} = \dfrac{\bar z}{\bar{z’}}$
Égalité de complexes, conjugué, opérations élémentaires - Exercice 1
Ce qu’il faut savoir faire :
Exercice 1
Étape 1 : On développe l’expression afin de faire apparaître la partie réelle et la partie imaginaire.
Étape 2 : On établit un système d’équations pour trouver les valeurs de \(a\) et de \(b.\)
Exercice 2
Étape 1 : On utilise la formule du cours pour trouver le conjugué (Si \(z= a + ib\) alors \(\bar z = a – ib\))
Étape 2 : On sait que \( \overline {z_1 \times z_2} = \bar z_1 \times \bar z_2 \)
Étape 3 : On développe en faisant attention que \( i^2 = -1 \).
Égalité de complexes, conjugué, opérations élémentaires- Exercice 2
Ce qu’il faut savoir faire :
Étape 1 : On remplace \(z_1\) par la valeur donnée dans l’énoncé.
Étape 2 : On multiplie au numérateur et au dénominateur par le conjugué de \(z_1\).
Étape 3 : On reconnait au dénominateur une identité remarquable \( a^2 – b^2 \).


