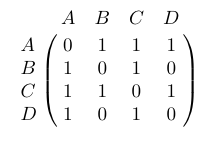Vocabulaire des graphes
Vocabulaire des graphes
Définition
Un graphe est un ensemble de points reliés entre eux.
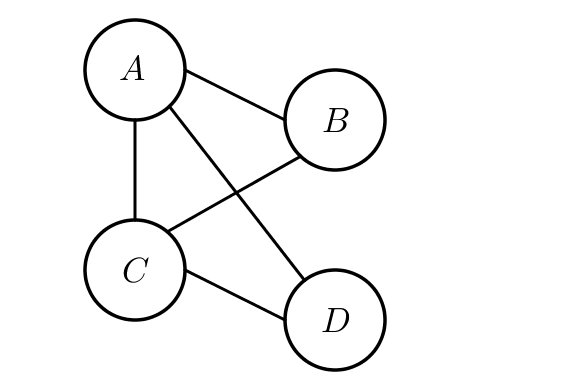
Dans la suite, on considéra comme exemple le graphe suivant.
Les points sont appelés des sommets. Le nombre total de sommets est appelé l’ordre : ici l’ordre vaut 4.
Deux sommets sont adjacents si ils sont reliés entre eux. Par exemple, $B$ et $D$ ne sont pas adjacents.
Les segments reliant deux sommets sont des arêtes.
Le degré d’un sommet correspond au nombre d’arêtes partant de ce commet. Par exemple, trois arêtes partent du sommet $A$ : $A$ est de degré 3.
Une chaîne de sommets est une liste de sommets reliés par des arêtes. Un cycle est une chaîne débutant par un sommet et terminant par ce même sommet. Par exemple $ABCD$ est une chaîne et $ABCA$ est un cycle.
La longueur d’une chaîne est le nombre d’arêtes composant cette chaine. Il ne faut donc pas compter le nombre de sommets ! Ainsi, la longueur de la chaine $ABCD$ est 3.
Un graphe est complet si tous les sommets sont reliés entre eux par une arête. Ici, $B$ et $D$ ne sont pas reliés entre eux, le graphe n’est donc pas complet.
Un graphe est connexe si tous les sommets sont reliés par une chaine quelconque. Ici le graphe est connexe.
Une chaine eulérienne est une chaine qui passe par chaque arête une seule fois : c’est le cas de la chaine $CDACBA$.
Un cycle eulérien est une chaîne fermée passant par chaque arête d’un graphe. Ici, il n’existe pas de cycle eulérien.
La matrice du graphe contient des 0 et des 1. Si il y a un 1 à l’intersection de la ligne $i$ et de la colonne $j$, alors il existe une arête reliant le sommet $i$ au sommet $j$. Sinon, aucune arête relit ces deux sommets et on l’indique alors par un 0.
Propriétés :
La somme des degrés des sommets vaut le double du nombre d’arêtes.
Si sur l’ensemble des sommets, seulement deux sont de degré impair, alors il existe une chaîne eulérienne. Cette propriété montre l’existence d’une telle chaîne mais ne la donne pas.
Si tous les degrés sont pairs, alors il existe un cycle eulérien.
Algorithme de Dijkstra
Algorithme de Dijkstra
Définition
L’algorithme de Dijkstra est un algorithme qui permet de calculer le plus court chemin entre deux sommets.
Exemple
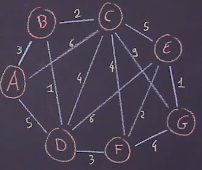
On considère le graphe suivant, et on souhaite trouver le chemin le plus court entre $A$ et $G$.
On dessine un tableau pour représenter les différentes étapes de l’algorithme et on écrit sur la première ligne le nom des sommets par ordre alphabétiques.
La dernière colonne représente le choix à l’issue de chaque étape de l’algorithme.
On part de $A$ : on dispose de trois possibilités : soit on va en $B$, soit en $D$ soit en $C$.
En dessous de chacun des ces sommets, on inscrit sur la premier ligne les poids de chaque arrête puis on choisit le sommet qui présente l’arrête de poids moindre.
Si aucune arrête relit deux sommets, on indique une distance infinie dans le tableau.
On choisit donc le sommet $B$, et on peut ensuite rejoindre le sommet $C$ ou le sommet $D$ : on ne peut pas revenir en $A$.
Lors de l’étape précédente, on avait choisit un chemin de longueur 3, donc à chacune des distances inscrites sur les arêtes, on ajoute la distance déjà parcourue pour atteindre le point $B$.
On suppose donc que l’on part de $D$. On remplit à nouveau la ligne de $D$.
On remarque que à l’étape précédente, on aurait pu passer par $C$.
On regarde donc les possibilités offertes par $C$ que l’on compare à celles offertes par $D$ : finalement, la distance la plus courte est celle allant en $F$ depuis $D$.
On choisit donc $F$ et on regarde les possibilités de chemin depuis ce sommet. On complète la fin du tableau en suivant le même principe.
Afin d’obtenir le chemin le plus court, il ne s’agit pas d’écrire tous les sommets inscrits dans la colonne “choix”, mais de remonter le raisonnement.
Ici, le chemin le plus court est $A-B-D-F-E-G$.
| $A$ | $B$ | $C$ | $D$ | $E$ | $F$ | $G$ | Choix |
| X | $3A$ | $6A$ | $5A$ | $\infty$ | $\infty$ | $\infty$ | $B$ |
| $5B$ | $4B$ | $\infty$ | $\infty$ | $\infty$ | $D$ | ||
| $8D$ | $10D$ | $7D$ | $\infty$ | on choisit $C$ depuis $B$ | |||
| $5B$ | $C$ | ||||||
| $10C$ | $9C$ | $14C$ | on choisit $F$ depuis $D$ | ||||
| $7D$ | $F$ | ||||||
| $9F$ | $11F$ | $E$ | |||||
| $10E$ | $G$ |