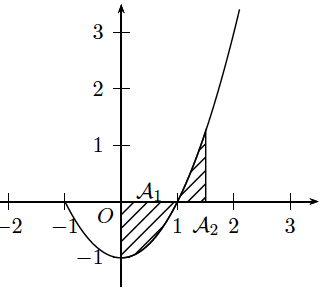Définition de l'intégrale
Définition de l’intégrale
Définition
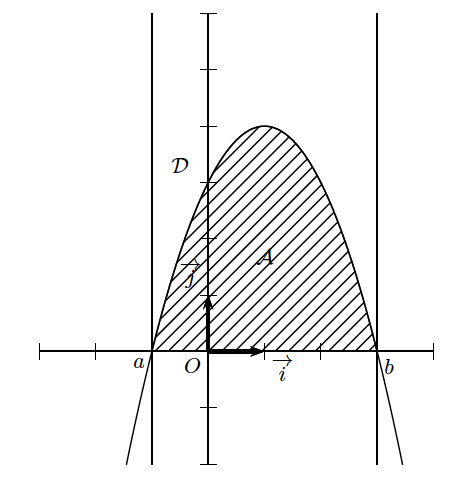
Soit (O,$\overrightarrow {i}$,$\overrightarrow {j}$) un repère orthonormé et une fonction $f$ continue et positive sur un intervalle $[a,b]$.
$\mathcal{D}$ est le domaine du plan délimité par $x$=$a$ , $x$=$b$, l’axe des abscisses et $\mathcal{C}_f$, la courbe représentative de la fonction $f$.
L’intégrale de $f$ sur $[a,b]$ notée $ \displaystyle \int \limits_a^b f (t)dt$ est l’aire $\mathcal{A}$ du domaine $\mathcal{D}$ exprimée en unités d’aire.
Exemple
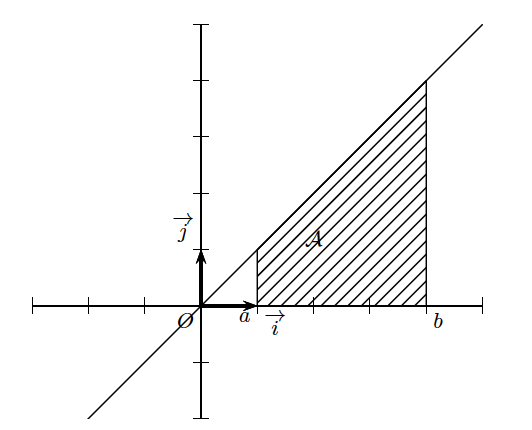
Calculer $I = \displaystyle \int_{1}^4 x dx = \int_{1}^4 t dt$ ($x$ et $t$ sont des variables muettes).
Etape 1 : On repère l’aire recherchée.
Etape 2 : On remarque qu’il s’agit d’un trapèze rectangle.
Etape 3 : La formule du calcul d’aire du trapèze rectangle est connue. On peut l’utiliser pour calculer l’intégrale :
$ A = \dfrac{(B + b) \times h}{2}$
$ A = \dfrac{5 \times 3}{2}$
Finalement, $I = \dfrac{15}{2}$ (exprimée en unité d’aire)
Cas d’une fonction non positive
Le signe d’une aire est toujours positif en revanche celui d’une intégrale va dépendre de la position de la courbe par rapport à l’axe des abscisses.
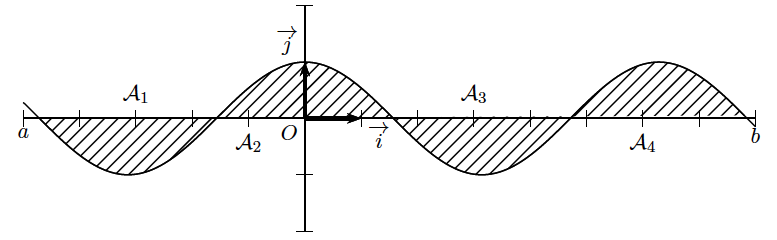
Ainsi, on pourrait avoir $I$:
$I= \displaystyle \int \limits_a^b f (t)dt=- \mathcal {A}_1+ \mathcal {A}_2-\mathcal {A}_3+\mathcal {A}_4$
Les $ \mathcal A_{i}$ sont les aires respectives des quatre domaines representés sur le graphique.
Exemple
Voici comment représenter: $\displaystyle \int \limits_0^{1,5} (x^2 -1)dx$
$I = \displaystyle \int \limits_0^{1,5} (x^2 -1)dx =- \mathcal {A}_1+ \mathcal {A}_2$
Définition de l'intégrale - Exercice
Calculons \(I = \int_{1}^4 x dx = \int_{1}^4 t dt\).
Étape 1 : On repère l’aire recherchée.
Étape 2 : On remarque qu’il s’agit d’un trapèze rectangle.
Étape 3 : La formule du calcul d’aire du trapèze rectangle est connue. On peut l’utiliser pour calculer l’intégrale :
\( A = \frac{(B + b) \times h}{2}\).
Propriétés de l'intégrale
Propriétés de l’intégrale
Linéarité de l’intégrale
Soit \(\lambda \in \mathbb{R}\) (\(\lambda\) est une constante), \(f\) et \(g\) deux fonctions continues sur \([a,b]\), on a :
\(\displaystyle\int_{a}^b \lambda f(x) + g(x)dx =\lambda \int_{a}^b f(x)dx+\int_{a}^b g(x)dx\)
Positivité de l’intégrale
Si \(f(x)\ge 0\) sur $[a;b]$ alors \(\displaystyle\int_{a}^b f(x)dx\ge 0\).
Croissance de l’intégrale
Si \(f(x)\le g(x)\) sur $[a;b]$ alors \(\displaystyle\int_{a}^b f(x)dx\le \int_{a}^b g (x)dx\).
Exemple
Écrire sous la forme d’une seule intégrale $J$=\(\displaystyle\int_{1}^e e^{4x} dx+ \int_{1}^e dx-2\int_{1}^e e^{2x}dx\).
On utilise la linéarité de l’intégrale pour regrouper les différents termes.
$J=\displaystyle\int_{1}^e (e^{4x} -2 e^{2x}+1)dx)$
$J=\displaystyle\int_{1}^e (e^{2x} -1)^2 dx)$
Propriétés de l'intégrale - Exercice
Linéarisons \(I = \displaystyle\int_{0}^2 (4x^3 + \frac{1}{2}x^2 + 1) dt\).
Étape 1 : On utilise la linéarité de l’intégrale pour la décomposer.
Écrire sous la forme d’une seule intégrale \(J = \displaystyle\int_{1}^e e^{4x} dx + \int_{1}^e dx – 2\int_{1}^e e^{2x} dx \).
Étape 1 : On utilise la linéarité de l’intégrale pour regrouper les différents termes.