Espace, droites et plans
Espace, droites et plans
Définitions
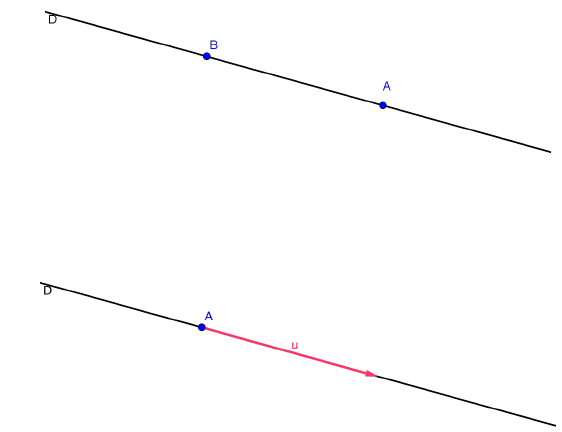
Une droite de l’espace peut être définie par :
- deux points ou
- un point et un vecteur directeur.
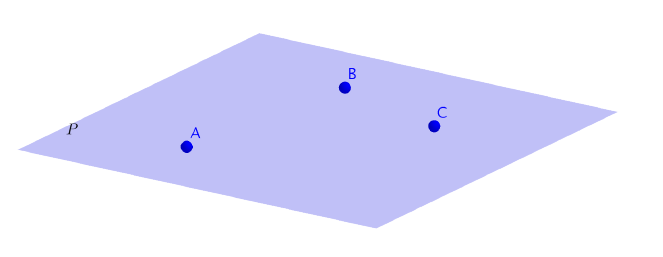
Un plan peut être défini par :
- trois points non alignés
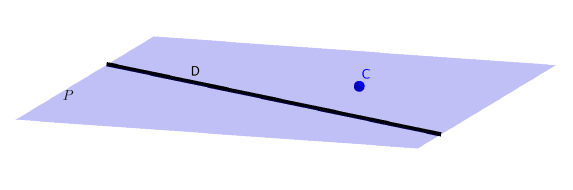
- Une droite et un point extérieur à la droite
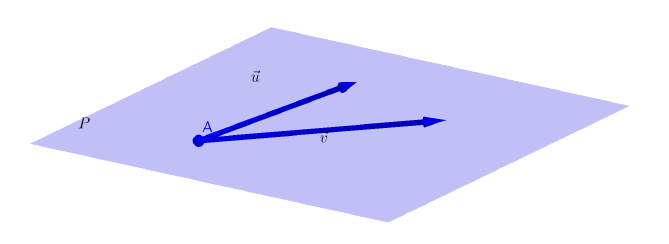
- Deux vecteurs non colinéaires et un point
Repères et coordonnées
Définition
On appelle repère de l’espace tout quadruplet $(O; \overrightarrow{i};\overrightarrow{j}; \overrightarrow{k}) $ constitué d’un point $O$ de l’espace et de trois vecteurs non coplanaires.
On note $(Ox)$ l’axe dirigé par $\overrightarrow{i}$, $(Oy)$ l’axe dirigé par $\overrightarrow{j}$ et $(Oz)$ l’axe dirigé par $\overrightarrow{k}$.
Lorsque les droites $(Ox)$, $(Oy)$ et $(Oz)$ sont perpendiculaires deux à deux, le repère est dit orthogonal.
Si de plus $||\overrightarrow{\imath}||=||\overrightarrow{\jmath}||=||\overrightarrow{k}||=1$, le repère est dit orthonormal.
Théorème
Soit $(O; \overrightarrow{i};\overrightarrow{j}; \overrightarrow{k}) $ un repère de l’espace.
Pour tout point $M$ de l’espace, il existe un unique triplet $(x ; y ; z)$ tels que
$\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$.
On dit alors que le point $M$ a pour coordonnées $(x ; y ; z)$ et on note $M(x;y;z)$.
Équation cartésienne d'un plan
Equation cartésienne d’un plan
Définition
Soient $a,b,c$ et $d$ quatre réels avec $a,b$ et $c$ tous nuls.
$\mathcal{P} :ax+by+cz+d=0$ est l’équation cartésienne d’un plan de l’espace.
Propriété
Tout plan $\mathcal{P}$ d’équation $ax+by+cz+d=0$ admet un vecteur normal non nul $\overrightarrow{n}(a;b;c)$.
La réciproque est vraie.

Exemples
1) Déterminer l’équation cartésienne du plan $\mathcal{P}$ passant par $A(4;0;-1)$ et normal à $\overrightarrow{n}(2;-1;3)$.
2) Soit $\mathcal{P}: 2x-4y+6z-9=0$.
Déterminer un vecteur $\overrightarrow{n}$ normal à $\mathcal{P}$ et un point $A$ du plan
Correction
- 1) Etape 1 : On définit l’équation cartésienne du plan à partir des coordonnées du vecteur $\overrightarrow{n}$.
On a: $\mathcal{P} : 2x-y+3z+d=0$.
- Etape 2 : On sait que $A \in \mathcal{P} $, on remplace $x, y$ et $z$ par les coordonnées du point $A$ appartenant au plan.
$2(4)-0+3(-1)+d=0$
- Etape 3 : On en déduit la valeur de $d$ et ainsi l’équation cartésienne du plan $\mathcal{P}$.
$d=-5$
On conclut que: $\mathcal{P} :2x-y+3z-5=0$.
- 2) Etape 1 : On définit un vecteur $\overrightarrow{n}$ normal à $\mathcal{P}$ à partir des coefficients de $x,y$ et $z$ de l’équation cartésienne.
$\overrightarrow{n}(2;-4;6)$ ou encore $\overrightarrow{n’}(1;-2;3)$ sont deux vecteurs normaux.
- Etape 2 : On fixe deux des trois inconnues afin de calculer les coordonnées pour que le point $A$ appartienne au plan.
On pose : $x=1$ et $y=2$ , avec $A \in \mathcal{P} $, on remplace : $2-8+6z-9=0$. $z=\dfrac{15}{6}=\dfrac{5}{2}$
On a alors : $A\left(1;2;\dfrac{5}{2}\right)$


