Définition du logarithme népérien
Définition du logarithme népérien
Définition
La fonction logarithme népérien est l’unique fonction $f$, définie et dérivable sur $]0; +\infty[$ qui vérifie $\begin{array}{l} f(1) = 0 \\ f'(x) = \dfrac{1}{x} \end{array}$
On remarquera ici que l’on définit la fonction $f$ à partir de sa dérivée.
En outre, on peut noter que l’on ne connaissait jusqu’à présent pas de fonction dont la dérivée valait $\dfrac{1}{x}$.
En supposant que le cours portant sur les intégrales a déjà été étudié, on peut alors définir la fonction logarithme népérien, que l’on note $\ln$ comme étant la primitive de $x \mapsto \dfrac{1}{x}$ sur $]0; +\infty[$ et qui s’annule en $1$.
Ainsi, pour tout réel $x > 0$,
$\ln x = \displaystyle \int_1^x \dfrac{1}{t} dt$
On notera que lorsque $x = 1$, $\ln 1 = \displaystyle \int_1^1 \dfrac{1}{t} dt = 0$.
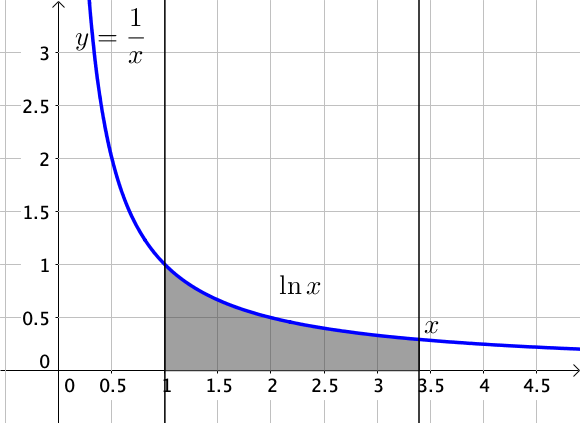
Graphiquement, la fonction $\ln x$ correspond à l’aire sous la courbe de la fonction inverse, comprise entre les droites verticales d’abscisse $1$ et $x$.
Propriétés analytiques
Propriétés analytiques
La fonction $\ln $ est définie et dérivable sur $]0;+\infty[$.
Pour tout réel $\displaystyle x>0, (\ln x)’= \dfrac{1}{x}$.
La fonction $\ln $ est continue et strictement croissante sur $]0;+\infty[$.
D’autre part,
$\ln (1)=0$
$\ln (e)=1$
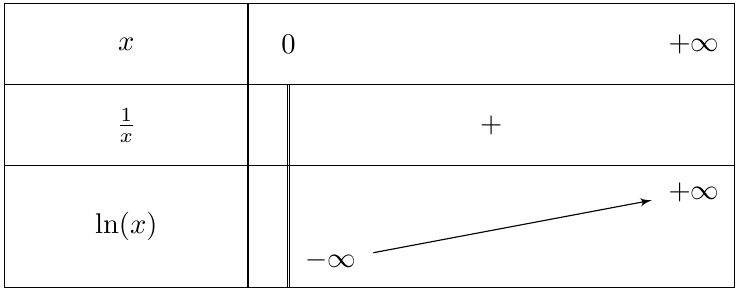
$\displaystyle\lim\limits_{x \rightarrow +\infty} \ln x= +\infty$
$\displaystyle \lim_{\substack{x \to 0\\ x > 0}} \ln x=-\infty$
Variations et représentation graphique
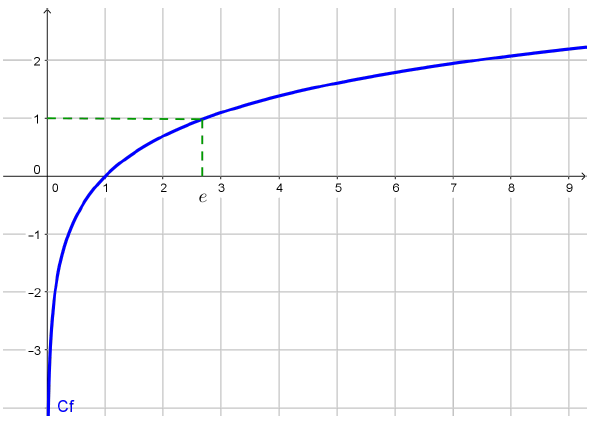
Propriétés algébriques
La fonction logarithme népérien
Définition
La fonction logarithme népérien est la fonction \(f\) définie et dérivable sur \(]0;+\infty[\) tel que
\(f(1)=0\) et \(f'(x)=\dfrac{1}{x}\)
\(\ln\) est la primitive de \(x\mapsto\dfrac{1}{x}\) sur \(]0;+\infty[\) qui s’annule en 1.
Propriétés algébriques
Pour tous réels $x>0$ et $y>0$ :
$\ln (xy)= \ln x+\ln y$
$\displaystyle \ln ( \displaystyle\frac{1}{x}) = -\ln x$
$\displaystyle \ln ( \displaystyle\frac{x}{y}) = \ln x-\ln y$
$\displaystyle \ln ( x^n) = n \ln x$ avec n $\epsilon$ $\mathbb{Z}$
Exemple :
Réduire : $A=\ln8-3\ln16$ et $B$= $\displaystyle \frac{4\ln9+5\ln27}{\ln3}$.
étape 1: On réécrit l’expression $A$ pour faire apparaître $\ln 2$.
$A=\ln 2^3-3\ln 2^4$
étape 2 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
$\displaystyle \ln (x^n)=n\ln x$ avec $\displaystyle n \in \mathbb{Z}$.
$A=3\ln 2-12\ln 2$
$A=-9\ln 2$
étape 3: On réécrit l’expression $B$ pour faire apparaître $\ln 3$.
$B$= $\displaystyle \frac{4\ln 3^2+5\ln 3^3}{\ln 3}$
étape 4 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
$\displaystyle \ln (x^n)=n\ln x$ avec $\displaystyle n \in \mathbb{Z}$.
$B$= $\displaystyle \frac{8\ln 3+15\ln 3}{\ln 3}$
On factorise par $\ln 3$ pour finir le calcul.
$B$= $\displaystyle \frac{23\ln 3}{\ln 3}$
$B$= 23
Autre exemple :
Simplifier : $C$= $\displaystyle \ln (x+3)+\ln 2-2\ln (x+1)$ en précisant l’intervalle d’étude.
étape 1 : On précise l’ensemble de définition de l’expression.
$x$ doit vérifier $x+3>0$ et $x+1>0$, c’est-à-dire :
$x>-3$ et $x>-1$.
La condition finale est donc: $x>-1$.
étape 2 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
- $ \ln (xy)=\ln x+\ln y$,
- $\ln (\displaystyle\frac{x}{y})=\ln x-\ln y$
- $\ln (x^n)=n\ln x$ avec $n \in \mathbb{Z}$
Ainsi,
$C$= $\displaystyle \ln (2x+6)-\ln (x+1)^2$
$C$= $\displaystyle \ln {\frac{2x+6}{(x+1)^2}}$


